2016
Cavity Quantum Electrodynamics, quantum critical phenomena ― Quantum phase transitions in driven-dissipative systems opened up a novel research area in the field of critical phenomena. These transitions lie beyond the standard classification of dynamical or equilibrium phase transitions, and define completely new universality classes. In an open quantum system, the critical behaviour appears in the state formed by the dynamical equilibrium of the external driving and dissipation processes. The abrupt symmetry breaking change of such a steady state takes place when the external control parameters are continuously tuned across the critical point. The correlation functions at the critical point are determined by non-equilibrium noise rather than thermal or ground-state quantum fluctuations. We demonstrated that criticality in a driven-dissipative system is strongly influenced by the spectral properties of the bath. We studied the open-system realization of the Dicke model, where a bosonic cavity mode couples to a fictious large spin formed by two motional modes of an atomic Bose-Einstein condensate. The cavity mode is driven by a high-frequency laser and it decays to a Markovian bath, while the atomic mode interacts with a colored bath. We revealed that the soft mode fails to describe the characteristics of the criticality. We calculated the critical exponent of the superradiant phase transition and identified an inherent relation to the low-frequency spectral density function of the colored bath. We showed that a finite temperature of the colored bath does not modify qualitatively this dependence on the spectral density function.
We investigated the possibility of the Dicke-type superradiant phase transition of an atomic gas. We described the ultrastrong coupling limit of the interaction between light and atoms within the regularized electric dipole gauge, in which we can take into account the short-range depolarizing interactions between atoms that approach each other as close as the atomic size scale. By using a mean field model, we find that a critical point does indeed exist, though the atom-atom contact interaction shifts it to a higher value than what can be obtained from the bare Dicke-model. We pointed out the proximity of the critical density to that of solidification, which leads to the conjecture that the system, at the critical density, goes over to the condensed rather than to the “superradiant” phase.
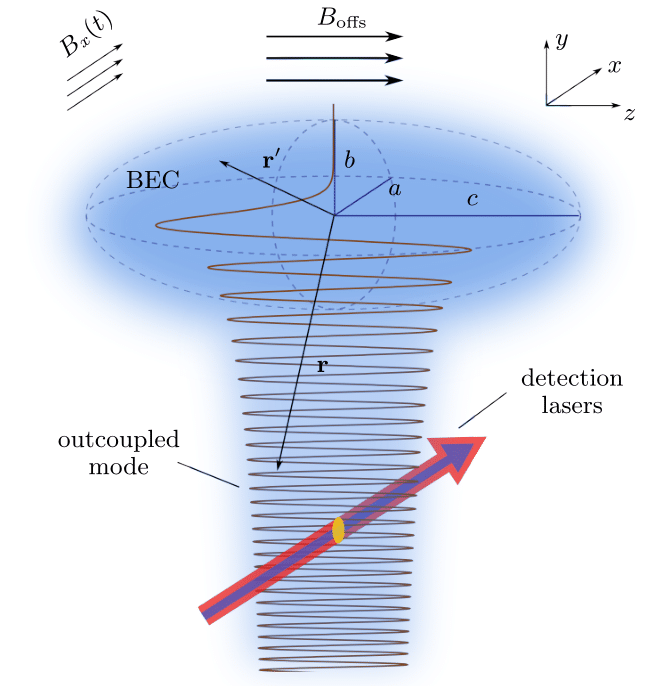
Ultracold gases, Bose-Einstein condensates ― Bose-Einstein condensates of ultracold atoms can be used to sense fluctuations of the magnetic field by means of transitions into untrapped hyperfine states. It has been shown recently that counting the outcoupled atoms can yield the power spectrum of the magnetic noise. As a continuation of our previous investigations, we calculated the spectral resolution function, which characterizes the condensate as a noise measurement device in this scheme. We used the description of the radio-frequency outcoupling scheme of an atom laser, which takes into account the gravitational acceleration. Employing both an intuitive and the exact three-dimensional and fully quantum mechanical approach, we derived the position-dependent spectral resolution function for condensates of different size and shape.
We investigated the magnetic properties of strongly interacting four-component spin-3/2 ultracold fermionic atoms in the Mott insulator limit with one particle per site in an optical lattice with honeycomb symmetry. In this limit, atomic tunneling is virtual, and only the atomic spins can exchange. We found a competition between symmetry-breaking and liquid-like disordered phases. Particularly interesting are the non-singlet valence bond states (where the valence bonds have non-zero magnetization) which are situated between the ferromagnetic and conventional valence bond phases. In the framework of a mean-field theory, we calculated the phase diagram and identified an experimentally relevant parameter region where a homogeneous SU(4) symmetric Affleck-Kennedy-Lieb-Tasaki–like valence bond state is present.
The classical ground states of the SU(4) Heisenberg model on the face-centered-cubic lattice constitute a highly degenerate manifold. We explicitly constructed all the classical ground states of the model. To describe quantum fluctuations above these classical states, we applied linear flavor-wave theory. At zero temperature, the bosonic flavor waves select the simplest of these SU(4) symmetry-breaking states, the four-sublattice-ordered state defined by the cubic unit cell of the fcc lattice. Due to geometrical constraints, flavor waves interact along specific planes only, thus rendering the system effectively two dimensional and forbidding ordering at finite temperatures. We showed that longer-range interactions generated by quantum fluctuations can shift the transition to finite temperatures.



