Introduction
The electromagnetic, weak, strong and gravitational forces are the four fundamental interactions of Nature. The first two, unified by the electro-weak quantum gauge theory, have been tested with high accuracy. The strong interaction is formulated also as a gauge theory but its strongly coupled nature circumvented its high precision tests, additionally, the gravitational interaction does not even have a satisfactory quantum formulation.
The gauge/gravity duality gives a hope to understand the strong interaction and quantum gravity in one turn as it connects gauge theories with string theory (including gravity). This duality is a conjecture, which relates strongly coupled gauge theories to semi-classical string theory and the deeply quantum string theory (gravity) to perturbative gauge theory.
The best chance to show the conjectured equivalence of gauge theories and string theory is the 't Hooft limit of the maximally supersymmetric gauge theory as in this limit integrability of the two dimensional string theory shows up.
In the last twenty years, motivated by particle physics problems, there have been intensive research and relevant progress in two dimensional integrable theories. These theories were solved in the bulk and also with boundaries by determining exactly the spectrum of particles together with their scattering data which were then used to calculate the full spectrum at any finite size.
The objective of our research is to apply the two dimensional integrable techniques to the holographic duality and as a result to describe strongly coupled gauge theories and investigate the quantum domain of string/gravity theory. In particular, we analyze the following topics.

The energies of string states are related to the anomalous dimensions of local gauge-invariant operators. The 't Hooft coupling of the gauge theory is proportional to the inverse of the string tension, while the number of colors is proportional to the inverse of the string coupling. In the planar (large color) limit, strings do not interact and one has to evaluate the string action on a two-dimensional cylindrically-shaped worldsheet. Due to the high number of symmetries, this effective two-dimensional field theory turned out to be integrable.
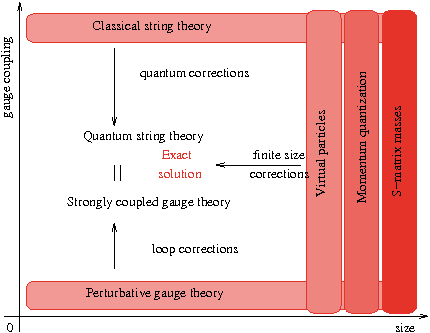
The various methods and their validity ranges are shown on the figure. For weak coupling, perturbative gauge theory is reliable. For large coupling, the string/gravity theory is (semi) classical, allowing a calculational basis. These two validity ranges have no overlap. On the other hand, the holographic correspondence is integrable, thus we can use integrable techniques starting from infinite size and systematically calculate all finite-size corrections. The final solution not only solves the spectral problem, but also gives evidence for the holography: gauge theory and string/gravity theory are two equivalent descriptions of the same phenomena.
Every conformal field theory (CFT) can be built up from its 2- and 3-point functions. The 2-point functions are completely determined by the anomalous dimensions of the operators, while the 3-point functions contain additionally a coupling constant dependent normalization. These 3-point functions correspond to form factors of defect/boundary creating operators and are related, on the string theory side, to the amplitudes of the process in which one big string splits into two small ones, or alternatively when two small strings join into a big one. Thus they provide the exact string interactions of the theory, which are required to develop the quantum theory of strings, namely string field theory (SFT). The amplitude is called the SFT vertex, which hasn't been calculated explicitly except for the flat background. We formulated axioms for this SFT vertex, which we solved in the pp-wave limit.
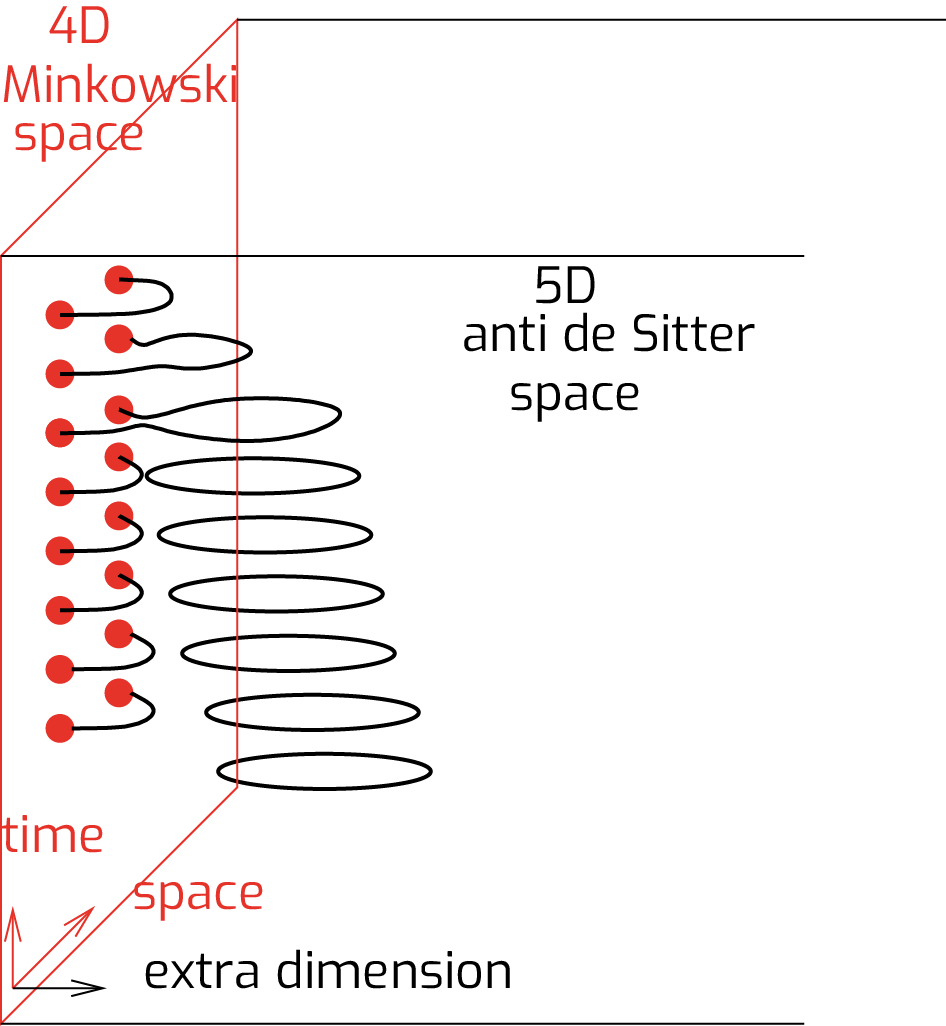
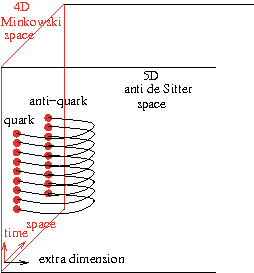
The maximally supersymmetric gauge theory is scale invariant, which forces the quark--anti-quark potential to be proportional to the inverse of the distance, as in quantum electrodynamics. So this theory is not confining; nevertheless, the coefficient (strength) of the potential depends nontrivially on the gauge coupling. Standard perturbative calculations determine this coefficient in terms of a power series giving a good approximation for small coupling. For large coupling, the holographic description can be used to calculate the string/gravitational partition function on the surface spanning the worldlines of the quark and anti-quark. At leading order, it amounts to evaluating the area of the minimal surface, while for finite coupling the quantum fluctuations must all be included, which is taken into account by a boundary thermodynamic Bethe Ansatz equation. We proposed a novel formulation of the BTBA equations, based on real chemical potentials and additional source terms, which allows a systematic weak coupling expansion. We expanded our equations to second (double wrapping) order and tested the results against direct two-loop gauge theory computations. We find complete agreement.
A brane--anti-brane system is an unstable open string system. It is believed that the branes annihilate with each other and decay into closed strings, however, there are no non-perturbative results supporting this idea in the literature for curved backgrounds. Our experience with integrable boundaries together with our insight into the gauge/string duality put us into a unique position to solve this relevant problem. We developed a complete description of the brane--anti-brane system both on the gauge theory and on the integrable model sides.