Gali Ádám kutatócsoportja két jelentős eredményt jelentetett meg a Nature Communications és Science Advances folyóiratokban együttműködésben David D. Awschalom kutatócsoportjával, amelyek a szilícium-karbidban előállított divakancia kvantumbitekkel kapcsolatosak.
Kvantuminformatikai alkalmazások kvantumbitek fizikai megvalósításain alapulnak. A kvantumbitek, röviden kubitek, olyan kontrolálható kétállapotú kvantum rendszerek, amelyek környezetükkel csak kis mértékben hatnak kölcsön. Félvezető anyagokban előforduló egyes paramágneses ponthibák spin állapotai olyan tulajdonságokkal bírhatnak, amelyek alkalmassá teszik ezen atomi méretű rendszereket kubit alkalmazások megvalósítására. Amennyiben ezen gazdaanyagba beágyazott ponthibák fluoreszkálnak és spinállapottól függő fluoreszcencia-intenzitást mutatnak, akkor az elektronspin állapotát optikai módszerrel lehet megállapítani, illetve az elektronspint egy adott spinállapotba lehet beállítani. Különösen érdekesek az olyan gazdaanyagok, amelyek a klasszikus félvezetőiparban széles körben használatosak, így a kvantumtechnológiai fejlesztések potenciálisan beágyazhatóak bejáratott félvezetőipari technológiai eljárásokba. Gali Ádám egy 2009-ben tartott konferencián közölte azt az elméleti eredményét [1], amely szerint a nagyteljesítményű elektronikában használt szilícium-karbid (SiC) széles tiltott sávú félvezető hordoz olyan paramágneses, spintől függő fluoreszcenciaintenzitású ponthibát, amelyet kvantumbitként lehetne hasznosítani. Ez a ponthiba két szomszédos vakanciából áll, melyet röviden divakanciának nevezünk [1. ábra]. Semleges töltésállapotban a divakancia egy S=1 paramágneses hiba, amely 1100 és 1300 nanométer közötti (infravörös) hullámhossz-tartományban lumineszkál.
Különösen a SiC ún. 4H kristálymódosulata elterjedt a félvezető iparban, melynek tiltott sávja kb. 3.2 eV, és gyakorta tartalmaz semleges divakanciát. A tökéletes 4H SiC-ban összesen négyfajta divakancia konfiguráció jelenhet meg, amelyekből kettő viszonylag magas szimmetriájú (ún. C3v), míg kettő közölük alacsonyabb szimmetriájú (ún. C1h). David D. Awschalom csoportja 2011-ben közölte a Nature folyóiratban azt az eredményét [2], amely demonstrálta a divakancia ponthibák kvantumbitként való alkalmazását. Ugyanebben a publikációban a négy lehetséges konfiguráció mellett (PL1-4) még két olyan jelet találtak (PL5 és PL6), amelyek nagyon hasonlítottak a divakancia jelére, de az eredetüket nem tudták azonosítani. Nagy pontosságú sűrűség-funkcionál elméleten alapuló számításokkal igazoltuk azt Ivády Viktor MTA Prémium Posztdoktori Ösztöndíjas kutatóval, hogy a rétegződési hibába ágyazott divakancia konfigurációk tulajdonságai jól korrelálnak a PL5 és PL6 centrumok ismert mágneses és optikai tulajdonságaival.
A tanulmányozott rétegződési hiba egy köbös réteg beépülése a tökéletes 4H SiC rácsba. Érdekes módon ezen atomi szélességű réteg beépülése jelentősen befolyásolja a lokális sávszerkezetet. Úgy viselkedik, mint egy kvantumvölgy, mert a vezetési sáv minimumnál 0,3 eV-tal mélyebb energiájú állapotokat hoz létre a rétegződési hiba körül, ahová töltéshordozó elektronok becsapdázódhatnak. Ez jelentősen befolyásolja az ezen rétegződési hibába beépült divakancia fotostabilitását, amely nagy fontosságú optikai gerjesztésen alapuló kvantumbit műveletek végrehajtása szempontjából.
A semleges PL1-4 divakancia fotogerjesztése közben – kis valószínűséggel – a negatív töltésű állapotba ionizálódhat szekvenciális két foton elnyeléssel az optikai gerjesztett állapoton keresztül [3, 4], amelynek következtében tartósan kikerül a spin kvantumbitet magvalósító töltés állapotból. A kvantumbit állapot csak egy alacsonyabb hullámhosszú fotogerjesztés hatására jöhet újból létre a negatív töltésű divakancia fotoionizációján keresztül [3,4]. Ez a jelenség két okból is káros: egyrészt, a kvantumbit állapotból kikerülve lelassul a kvantumbit műveletek végrehajtása, mert folyamatosan vissza kell ionizálni a ponthibát; másrészt, bonyolultabb kísérleti elrendezést igényel két különböző hullámhosszú lézer alkalmazása.
Ezzel szemben a PL5-6 kvantumbitekre azt jósolja a javasolt modell, hogy a két fotonnal történő ionizáció után a semleges divakancia fotogerjesztésénél használt hullámhosszú lézerrel azonnal visszaionizáljuk a negatívan töltött PL5-6 divakanciát a semleges állapotba, ugyanis a negatívan töltött állapot ionizációs küszöbenergiája 0,3 eV energiával alacsonyabb a rétegződési hiba fent említett kvantumvölgyes elektronszerkezete miatt, mint a tömbi részben tartózkodó PL1-4 divakancia konfigurációké [2. ábra]. Ennek következtében a fotogerjesztés túlnyomó időtartama alatt a PL5-6 divakancia konfigurációk a kvantumbit állapotukban tartózkodnak. Ez összhangban van egy korábbi kísérleti megfigyeléssel [3].
A sűrűségfunkcionál-elméleten alapuló modell igazolása érdekében a svéd Linköping Egyetem munkatársai előállították a divakanciát tartalmazó SiC anyagot, amelyet a Chicago Egyetem munkatársai az Argonne Nemzeti Laboratóriumban a legmodernebb szinkrotron röngenforrással vizsgálták meg közel 1 nanométeres térbeli felbontással. Munkatársaink a röntgen-diffrakciós módszerekkel igazolták azt, hogy a PL5-6 kvantumbiteket tartalmazó SiC-ban valóban előfordulnak azok a Si-C kettősréteg beékelődések, amelyeket az elméleti modell megjósol. Ez a kísérleti eredmény megerősítette a modell érvényességét. A fenti eredményeket általánosíthatjuk más típusú kvantumbitekre 4H SiC-ban, illetve bármilyen más anyagban, ahol a rétegződési hibák hasonló kvantumvölgyeket hoznak létre töltéshordozók számára. Gali Ádám és munkatársai ezt a tanulmányt „Stabilization of point-defect spin qubits by quantum wells” címmel a Nature Communications folyóiratban publikálták [Ivády et al., Nature Communications 10, 5607 (2019) „Stabilization of point-defect spin qubits by quantum wells”].
A PL3 és PL4 konfigurációk az alacsony szimmetriájú divakancia konfigurációk. Ezek közül David D. Awschalom csoportja a PL4 centrumot vizsgálta meg mikrohullámú váltakozó elektromos tér jelenlétében. Alacsony hőmérsékleten közel rezonáns optikai gerjesztést alkalmazva azt figyelték meg, hogy az így meghajtott divakancia kvantumbit Landau-Zener-Stückelberg (LZS) interferenciát mutat, azaz az elektronspin koherensen csatolódott a mikrohullámú elektromos térhez [3. ábra]. A jelenség megértéséhez az elektronszerkezet pontos ismeretére volt szükség, amelyet nem tártak fel eléggé részletesen szemben a magas szimmetriájú esetekkel [5]. Gali Ádám és kutatócsoportja sűrűségfunkcionál-elméleten alapuló módszereket használt az alacsony szimmetriájú konfigurációk azonosítása és vizsgálata céljából. Korábbi munkákban kimutatták (az utolsót ld. itt [6]), hogy a PL4 divakancia az a konfiguráció, amelyben a szénvakancia a köbös alrácsban, míg a szilíciumvakancia a hexagonális alrácsban tartózkodik [6]. Ebben az alacsony szimmetriájú konfigurációban az elektronspin kvantálási tengelye nagyjából 70,5°-ot zár be a hexagonális kristály forgási szimmetriatengelyével (c-tengely). Számításokkal sikerült megállapítani a gerjesztett állapotban a degenerált állapotok kristálytér-felhasadásának mértékét. Ebből lehetett arra következtetni, hogy a kristálytér felhasadás értéke teljesen elnyomja a gerjesztett állapotban a spin-pálya kölcsönhatást. Továbbá, a számításokból arra lehetett következtetni, hogy egy olyan effektív spin hamiltoni operátort lehet felírni erre a konfigurációra, amelyben a spin kvantálási tengely „hamis” szimmetria forgási tengelyként használható, amelyhez a kristályteret hozzá kell adni. Ebből kiindulva az LZS interferencia-képet jól lehetett magyarázni. Ezzel az eredménnyel egyben receptet adtunk arra is, hogyan kell a hasonló alacsony szimmetriájú kvantumbitek tulajdonságait analizálni és számítani. David D. Awschalom és Gali Ádám kutatócsoportjai a fenti eredményeket „Electrically driven optical interferometry with spins in silicon carbide” címmel a Science Advances folyóiratban publikálták [Miao et al., Science Advances 5, eaay0527 (2019) „Electrically driven optical interferometry with spins in silicon carbide”].
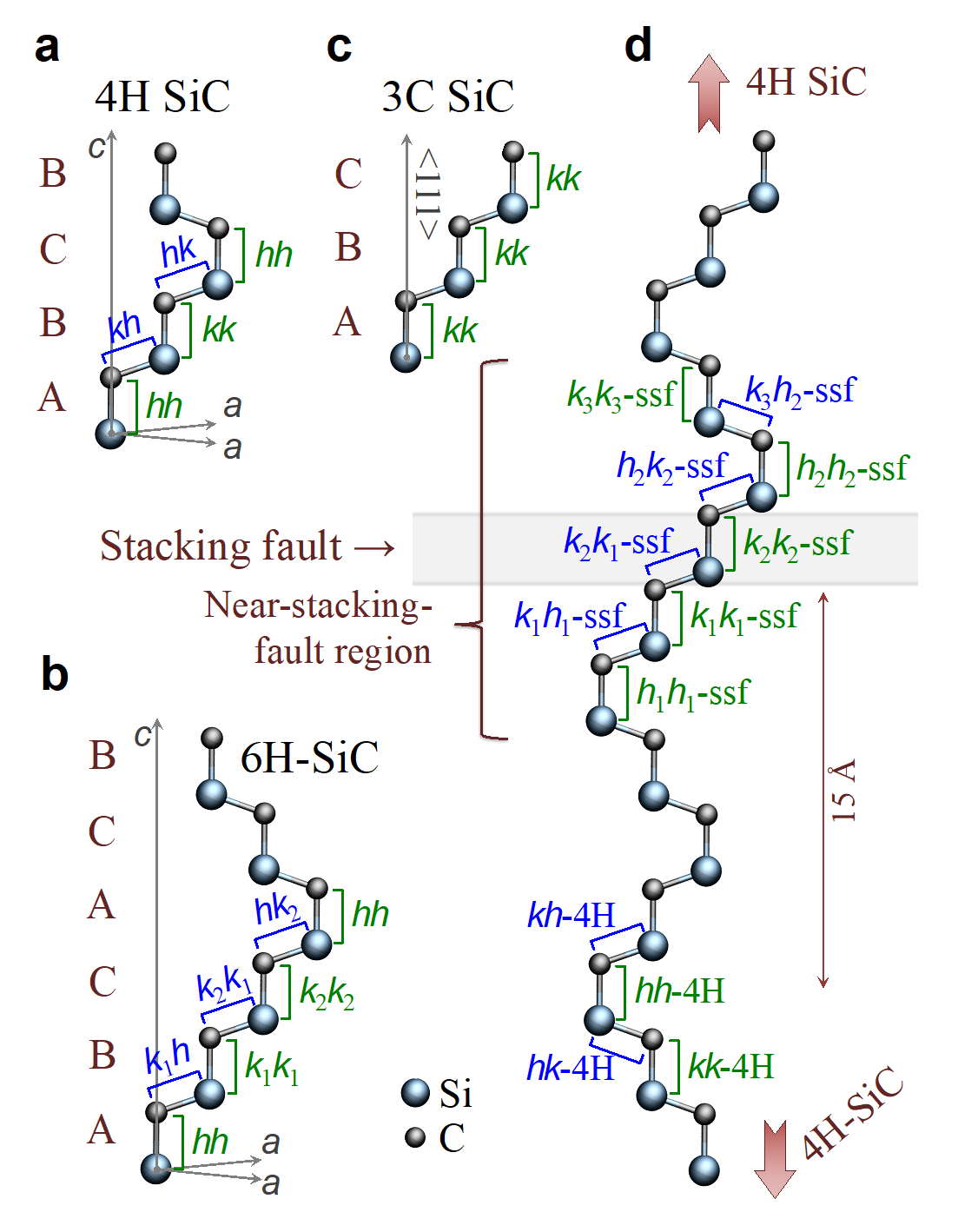
1. ábra A szilícium-karbid (SiC) rács 4H módosulata. „h” és „k” Si-C kettősrétegeket különböztetünk meg (rendre ún. hexagonális és köbös rétegződés), amelyeknek az elnevezését a rétegződési rétegek egymáshoz való viszonya adja. A divakancia hibát úgy képzelhetjük el benne, hogy a SiC rácsból eltávolítunk két szomszédos atomot. Ez négy lehetséges konfigurációt ad, hh, kk, kh és hk.
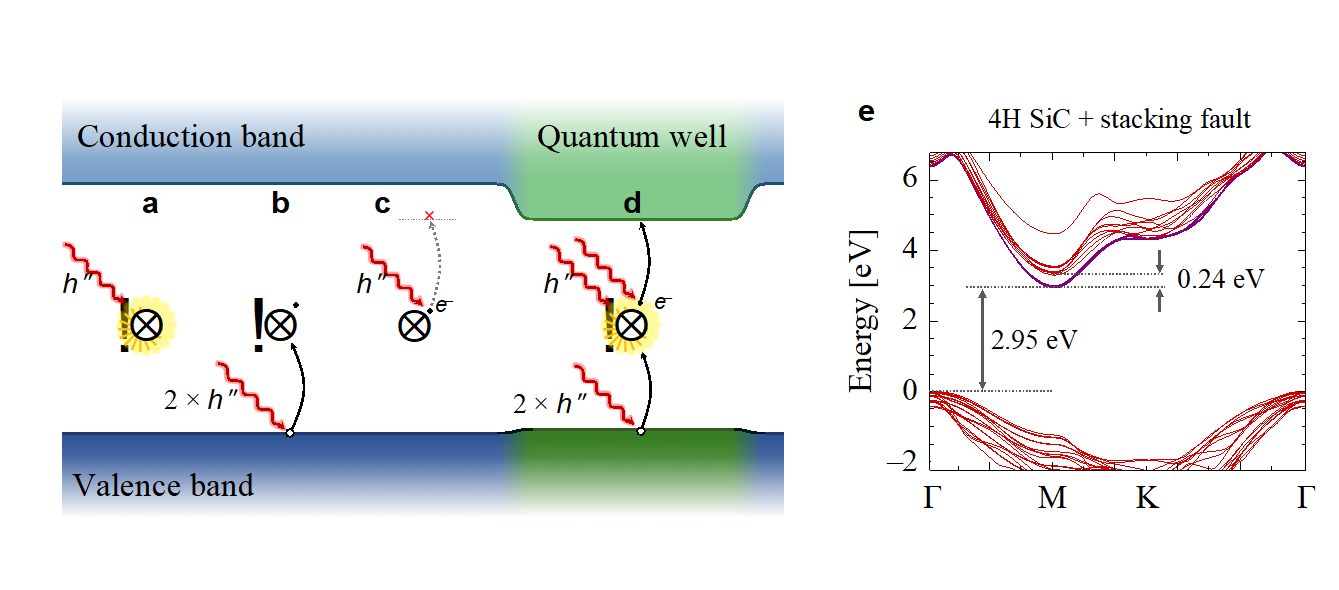
2. ábra. A PL5 és PL6 divakancia konfigurációk fotostabiltásának sematikus magyarázata. a, b és c ábrák összefoglalják a PL1-4 tömbi divakancia konfigurációk legfontosabb optikai gerjesztési folyamatait. a Gerjesztés hatására a divakancia ponthiba lumineszkál. b Kétfoton elnyelés hatására a ponthiba ionizálódik és ez által a kubit állapot megszűnik. c A gerjesztéshez használt foton energia nem elegendő, hogy visszaállítsa a kubit állapot elektronkonfigurációját. Ilyen esetben a PL1-4 divakancia ponthibák hosszú időre alkalmatlanná válhatnak kubit műveletek végrehajtására. d Egy rétegződési hibák által keltett kvantumvölgy csökkenti a vezetési sávél energiáját, - PL5-6 divakancia szerkezeti hibák esete - ami segítheti a kubit állapot visszaállítását nagyobb energiájú gerjesztő fény alkalmazása nélkül is.
3. ábra. a A PL4 hiba ábrája közelről és a hozzátartozó fotolumineszcencia spektrum, ahol a nyíl a zérusfonon-vonal hullámhosszát mutatja, és b a hozzátartozó LZS interferenciakép.
A kutatásokat az NKFIH Kutatói Kiválósági Program Élvonal programja támogatja (Kvantum-koherens anyagok projekt, KKP129866), illetve az EU QuantERA program (Nanospin projekt; NKFIH NN127902) és az EU Bizottság H2020 programja (ASTERIQS projekt; projektszám: 820394).
Irodalomjegyzék:
[1] A. Gali, A. Gällström, N. T. Son, and E. Janzén, Theory of neutral divacancy in SiC: a defect for spintronics, Mater. Sci. Forum 645-648, 395-397 (2010); A. Gali, Time-dependent density functional study on the excitation spectrum of point defects in semiconductors, phys. status solidi b 248, 1337-1346 (2011).
[2] W. F. Koehl, B. B. Buckley, F. J. Heremans, G. Calusine, and D. D. Awschalom, Room temperature coherent control of defect spin qubits in silicon carbide, Nature 479, 84–87(2011).
[3] G. Wolfowicz, C. P. Anderson, A. L. Yeats, S. J. Whiteley, J. Niklas, O. G. Poluektov, F. J. Heremans, and D. D. Awschalom. Optical charge state control of spin defects in 4H-SiC. Nat. Commun. 8, 1876 (2017).
[4] B. Magnusson, N. T. Son, A. Csóré, A. Gällström, T. Ohshima, A. Gali, and I. G. Ivanov, Excitation properties of the divacancy in 4H-SiC, Phys. Rev. B 98 195202 (2018).
[5] D. J. Christle, P. V. Klimov, C. F. de las Casas, K. Szász, V. Ivády, V. Jokubavicius, J. Ul Hassan, M. Syväjärvi, W. F. Koehl, T. Ohshima, N. T. Son, E. Janzén, Á. Gali, and D. D. Awschalom, Isolated Spin Qubits in SiC with a High-Fidelity Infrared Spin-to-Photon Interface, Phys. Rev. X 7, 021046 (2017).
[6] J. Davidsson, V. Ivády, R. Armiento, N. T. Son, A. Gali, and I. A. Abrikosov, First principles predictions of magneto-optical data for semiconductor point defect identification: the case of divacancy defects in 4H–SiC, New J. Phys. 20, 023035 (2018).



