Instantaneous, parallel measurement of the Kossel line pattern of single crystals excited by X-ray free-electron lasers enables the determination of 3-dimensional atomic structure in femtoseconds.
The arrangement of atoms in a solid is crucial to understanding the material’s properties. X-ray diffraction was the first and is still a widely used method to study the atomic structure of crystals. The time required for a diffraction measurement is determined by the complexity of the structure to be determined, the size of the crystal, the experimental technique and the properties of the X-ray beam. The 4th generation X-ray sources, X-ray free-electron lasers (XFELs), in a single, few fs long (10-15s) pulse provide about the same amount of usable X-ray photons as a laboratory X-ray source operating continuously for several hours. Because of this, one would think that the time required to perform a diffraction measurement could be reduced accordingly. But this is not the case. A conventional single-crystal diffraction measurement cannot be arbitrarily shortened and performed with a single XFEL pulse. This is because the Bragg reflections are usually recorded serially while the crystal is rotated in the incident beam. However, it is impossible to change the orientation of the crystal, especially in a controlled manner, within femtoseconds.
In a paper published in the journal Nature Communications , Gábor Bortel, Miklós Tegze and Gyula Faigel presented and demonstrated an experimental technique to measure a large number of Bragg reflections of a single crystal in parallel without rotating the sample. Thus, it is possible to determine the full 3-dimensional structure of a crystal using a single XFEL pulse. This method relies on the Kossel lines already observed and explained at the dawn of X-ray research: in the process, a spherical radiation field from a secondary X-ray source hits the crystal planes from "all directions" - thus eliminating the need to rotate the crystal - but only the components satisfying the Bragg condition are reflected, forming a cone-shaped radiation field that leaves the sample. The secondary sources are some atoms in the crystal itself, which are excited by the XFEL pulse and emit fluorescence radiation at slightly lower X-ray energies. Since these internal source atoms are part of the crystal structure, their location is identical in all unit cells, which also results in an interference signal in the intensity profile of the Kossel lines, which also encodes the phase of the structure factor of the reflection.
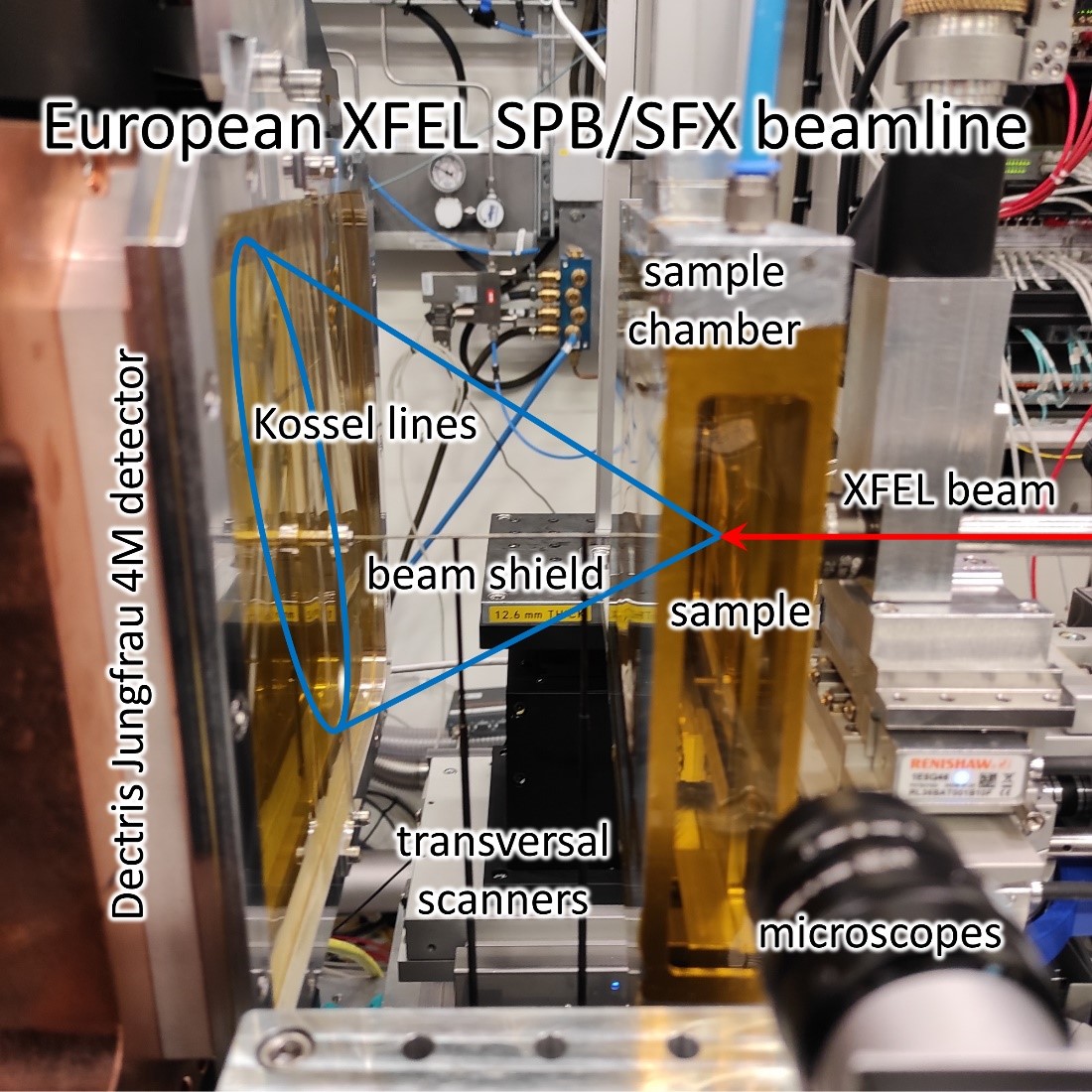
In a demonstration experiment at the European XFEL facility, a single XFEL pulse of ~25 fs length and ~1 mJ energy excited Ga atoms in GaAs and GaP single crystal samples, and Kossel lines appeared as cone slices on the surface of a flat detector. The samples were thin slices of semiconductor-grade single crystals to measure high-contrast, high-quality Kossel lines. The Kossel line pattern formed by the fluorescence emission of the secondary source atoms of the sample was recorded by a 4 MPixel detector integrating during the pulse time.

The Kossel line pattern contains first and foremost geometric information. The axis and the angle of the cone for each Kossel line define a reciprocal lattice vector and ultimately determine the crystal lattice. Due to the sufficiently high angular resolution of the recorded pattern, the fine interference signal also allows the determination of the amplitude and phase of the structural factors. This information leads to an elegant solution to the phase problem, since the electron density within the unit cell can be determined by Fourier synthesis.
The development and practical implementation of the new measurement principle opens up new possibilities for the investigation of structural transformations that can be induced for short periods of time under extreme conditions, or allows for a complete structure determination for each test pulse in pump-probe measurements. Beyond this, the significance of the results lies in the fact that the new measurement principle allows a complete measurement to be performed instantaneously and the method also offers a substantially new solution to the phase problem based on experimental information.



