Kvantumoptika "Lendület" Kutatócsoport

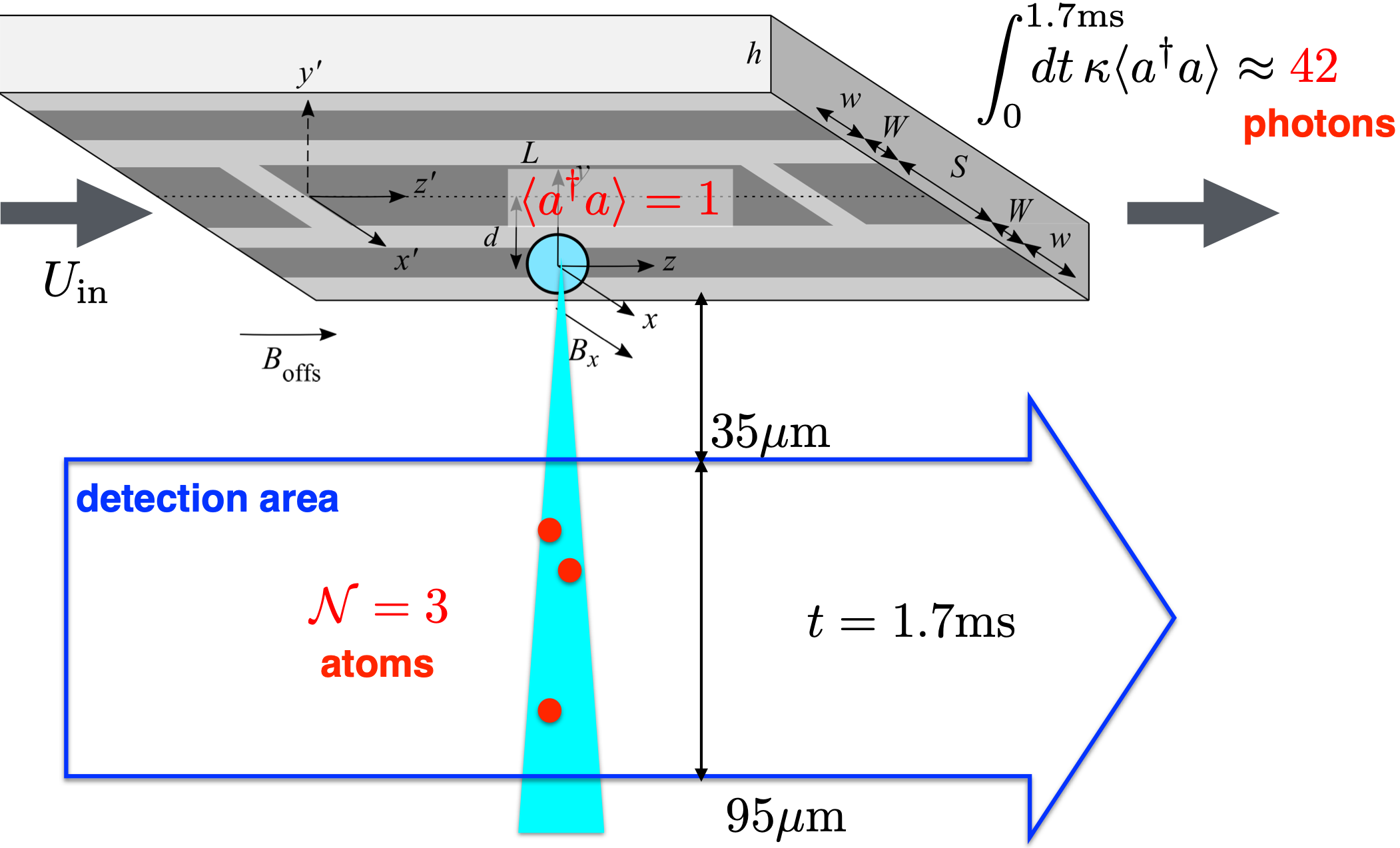
2024

Peter Domokos, Thomas W Clark, András Dombi, Balázs Endrész, Bence Gábor, Árpád Kurkó, Dávid Nagy, Bálint Sárközi, Alexandra Simon, Dániel Varga, András Vukics, Francis I B Williams

Experiment on Cavity Quantum Electrodynamics with cold Rb atoms. — We showed that an optimized loading of a cold ensemble of rubidium-87 atoms from a magnetic trap into an optical lattice sustained by a single, far-red-detuned mode of a high-Q optical cavity can be efficient despite the large volume mismatch of the traps. The magnetically trapped atoms are magnetically transported to the vicinity of the cavity mode and released from the magnetic trap in a controlled way meanwhile undergoing an evaporation period. Large number of atoms get trapped in the dipole potential of the cavity mode for several hundreds of milliseconds. We monitor the number of atoms in the mode volume by a second tone of the cavity close to the atomic resonance. While this probe tone can pump atoms to another hyperfine ground state uncoupled to the probe, we demonstrate state-independent trapping by applying a repumper laser.

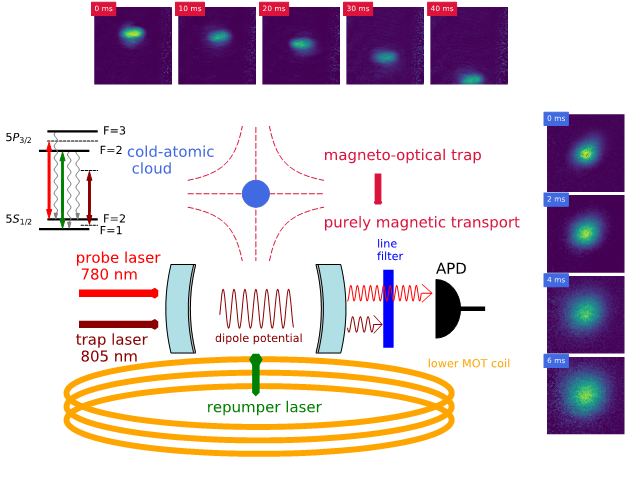
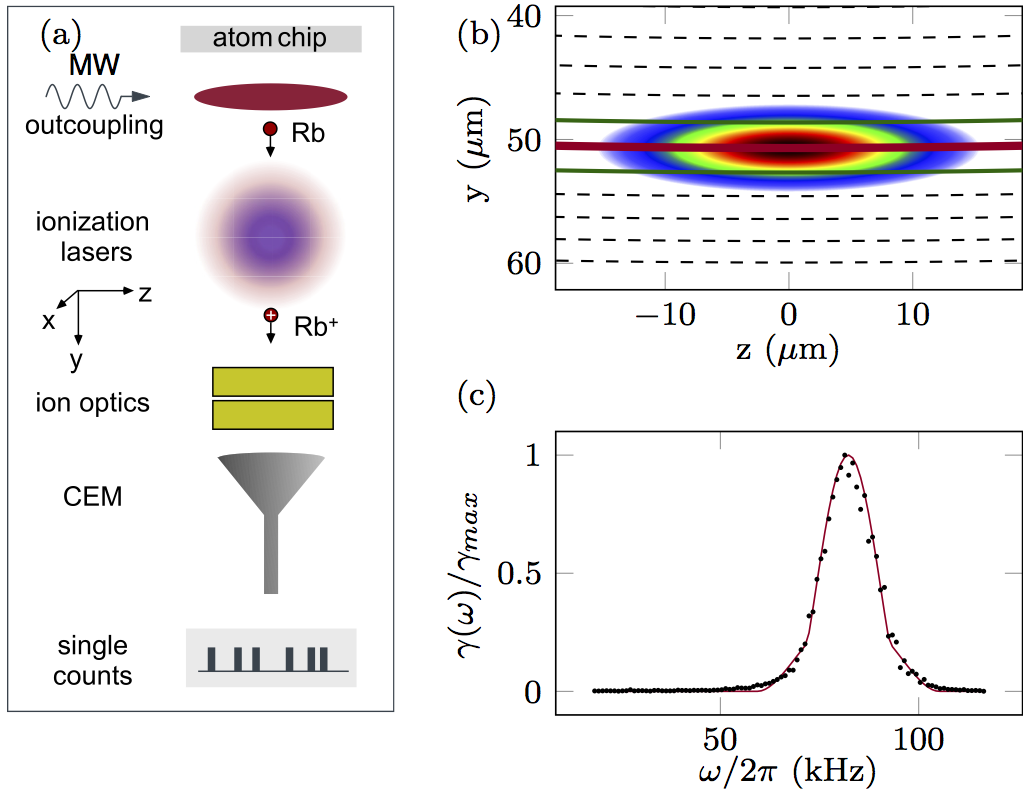
Fig. 1. Schematic of the experimental apparatus. A cold ensemble of 87Rb is created by magneto-optical trapping and polarization-gradient cooling. After optical pumping into trapped states in a magnetic quadrupole configuration, the cloud is magnetically transported downwards into the optical cavity (illustrated by the horizontal sequence of absorption images). The cavity has two modes relevant to the experiment: (1) the optical lattice mode far-red-detuned (≈805nm, dark red arrow) from the atomic resonance (2) a mode close to the atomic resonance (red arrow) used for monitoring the intra-cavity atom number via the dispersive effect of the atoms. On the cavity output, the trap light is filtered out, while the intensity of the probe light is monitored by an avalanche photodetector. To recover the atoms depumped into the 𝐹 =1 hyperfine ground state uncoupled to the probe, we can optionally apply a repumper tone (green arrow). The relevant atomic levels and the laser tones are depicted in the top left corner of the figure, using the same colourcode for the latter as described above. The vertical sequence of absorption images shows the expansion of the atomic cloud (time of flight) upon switching off the magnetic trap.
 
 

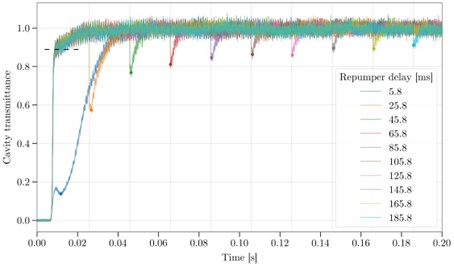
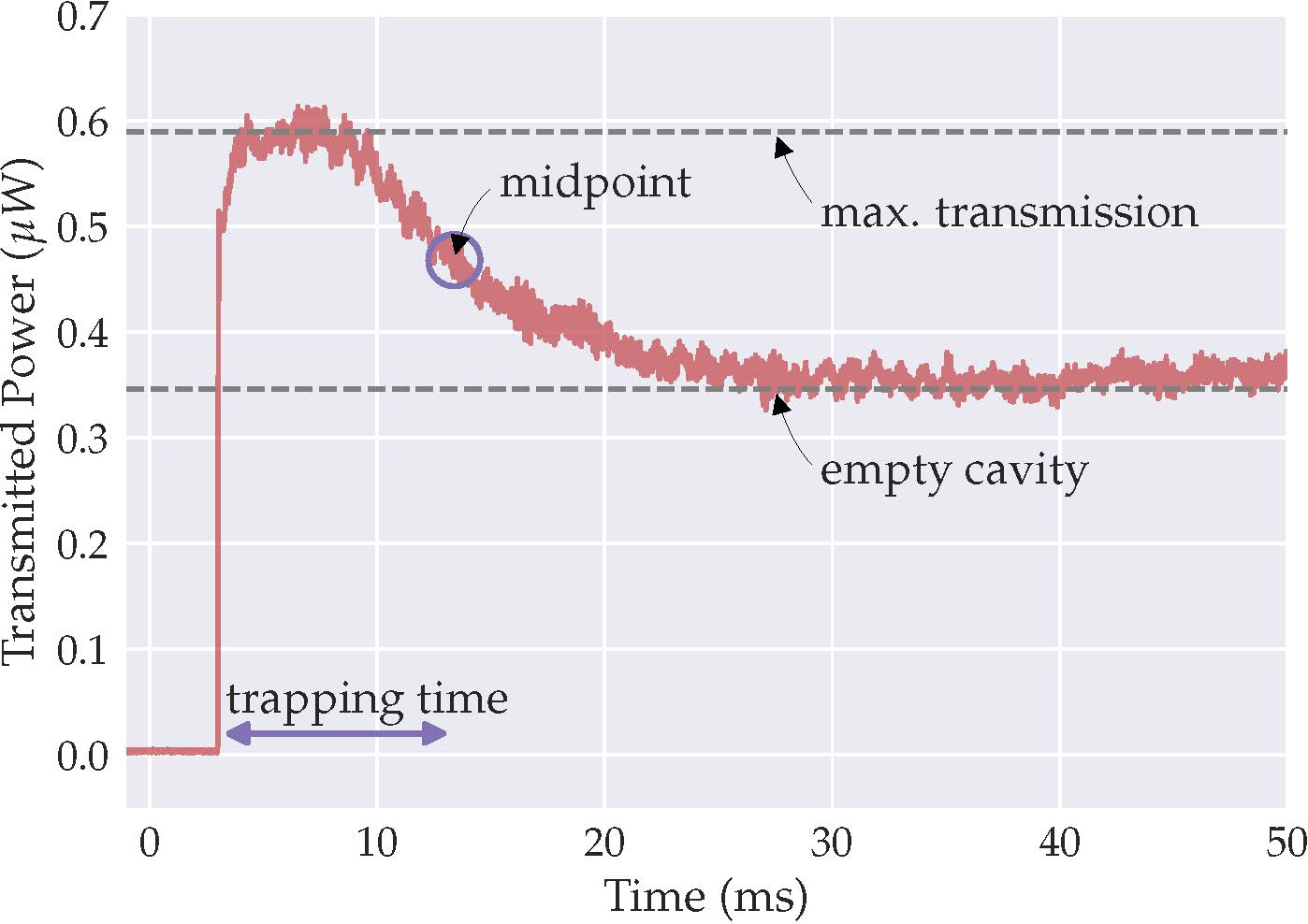
Figure 2. Stroboscopic estimate of the atom number. Each curve is an average of 10 runs and corresponds to a different delay of the repumper exposure. The probe light is opened at 7 ms in every run. The abrupt rise from 0 to 0.9  (black dashed line) in the beginning of all the curves but the blue one corresponds to the timescale of the shutter opening, and to the depumping process to the F=1 state. The transmittance does not reach its maximum because of the atoms falling into the interaction volume from the cloud surrounding the mode. When the repumper is turned on, the transmittance drops suddenly, due to the dispersive shift of the atoms which recover from F=1 to F=2. The averages around the minima at these dips (denoted by coloured dots) are used to determine the effective number of atoms. Concerning the blue curve, the initial fast rise remains below 0.2, because in this case the repumper is already on when the probe light enters the cavity, and hence the depumping is disabled. The small dip afterwards can be explained with the trapping effect of the probe light itself. All of the curves, including the blue one, once they reach their minimum, tend to T=1, as the cavity field and the repumper together heat the atoms out of the trap. The noise visible on the curves is dominated by Poissonian shot noise. 
 

Reference
D Varga, B Gábor, B Sárközi, KV Adwaith, D Nagy, A Dombi, TW Clark, FIB Williams, A Vukics, P Domokos, Loading atoms from a large magnetic trap to a small intra-cavity optical lattice, 

Physics Letters A 505 (2024) 129444

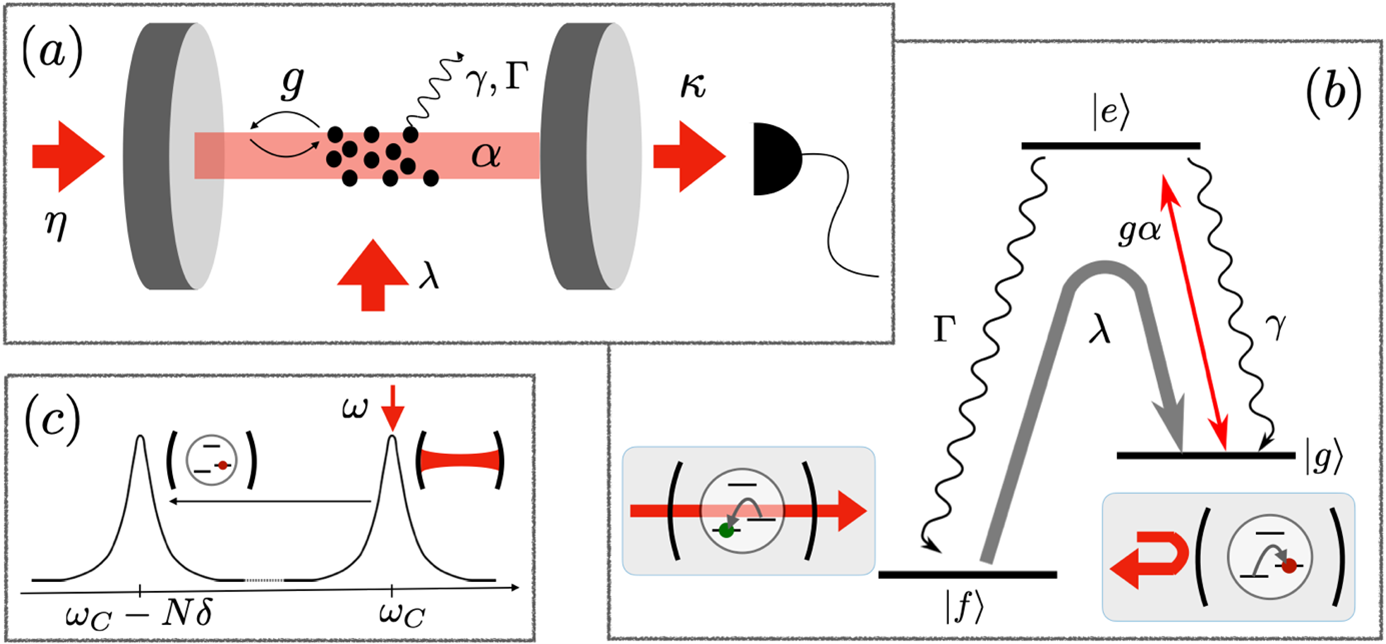
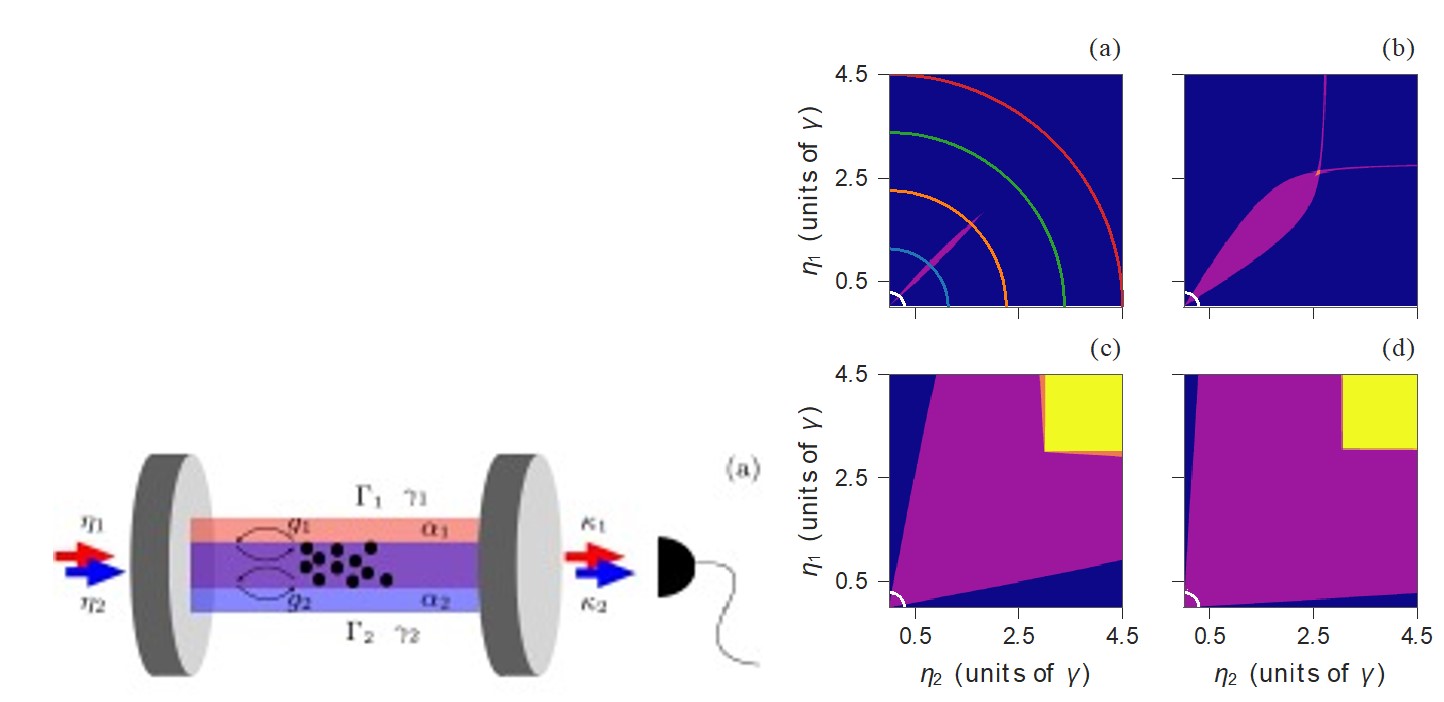
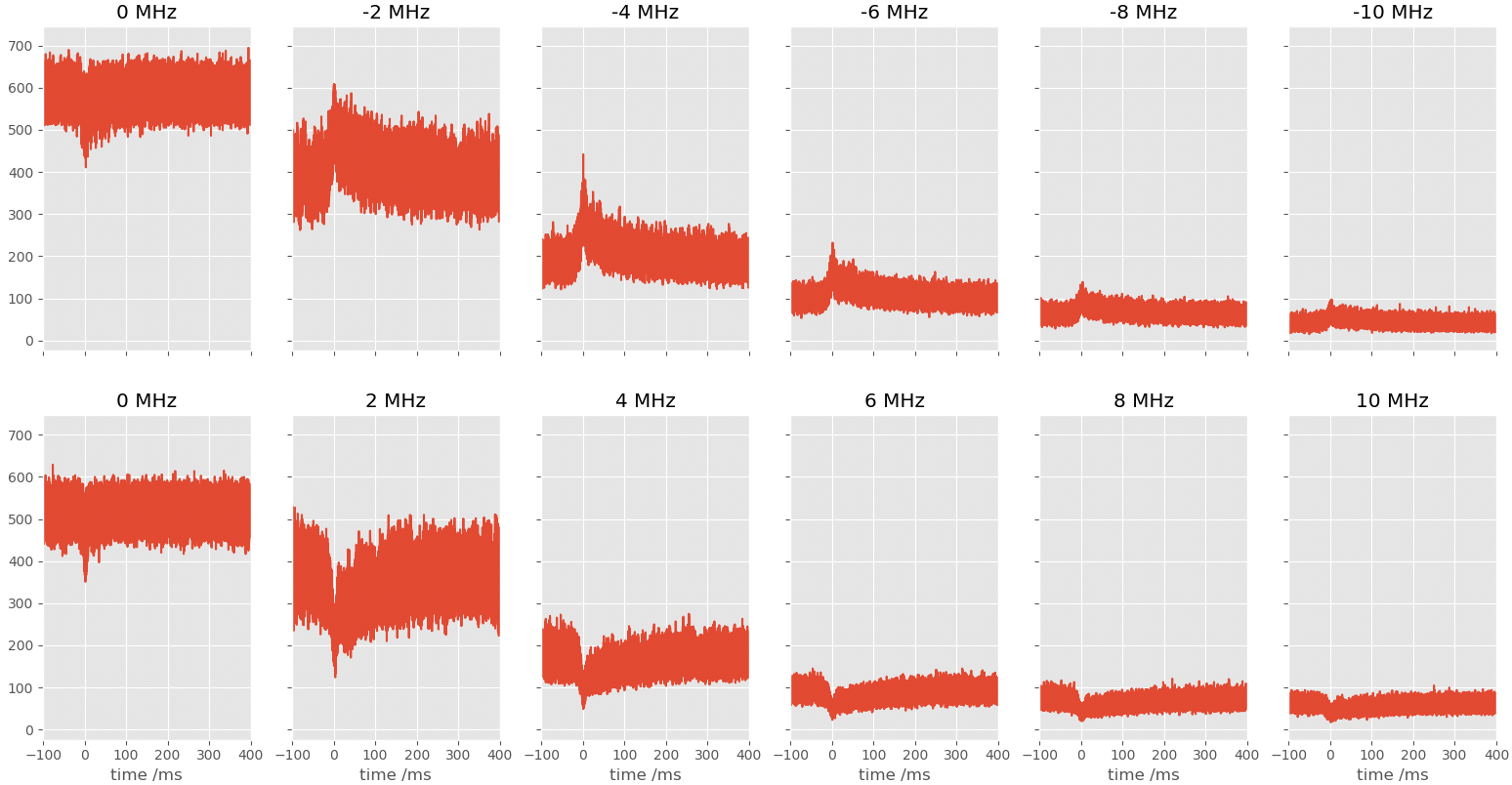
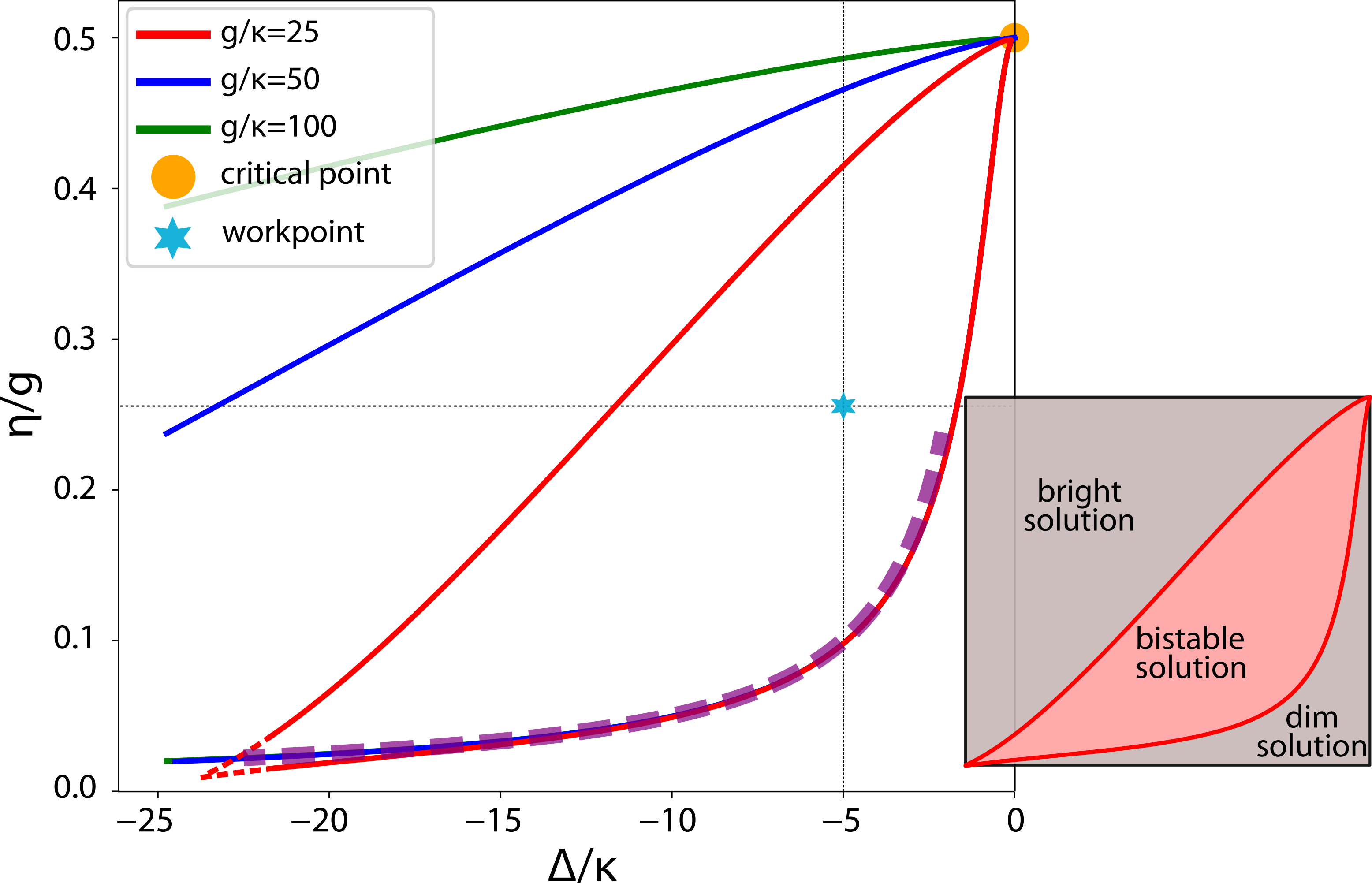
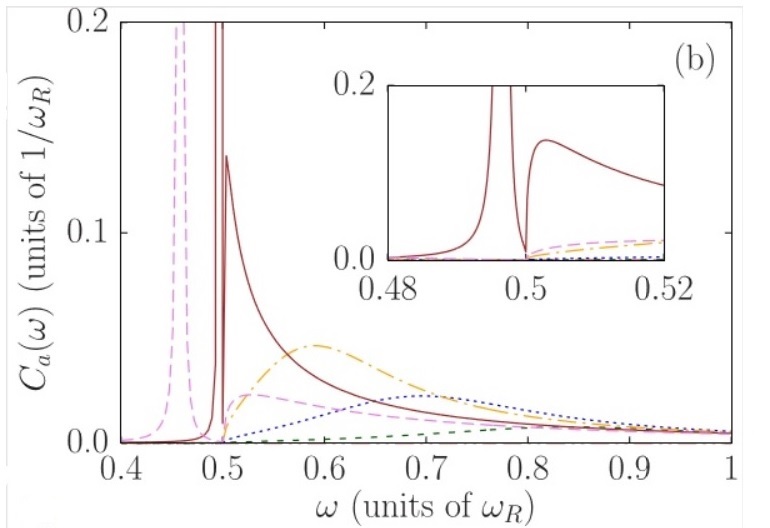
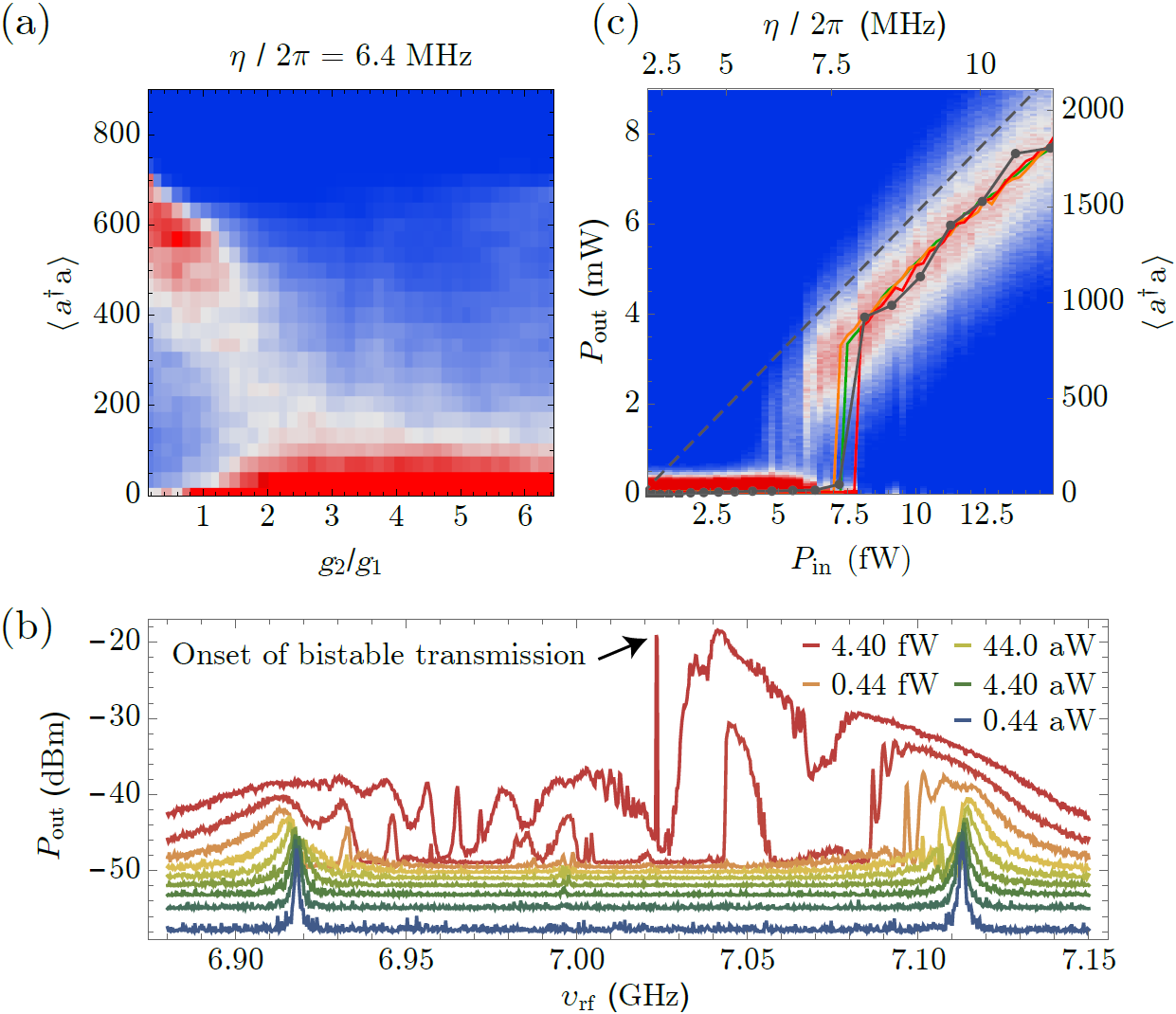
The photon-blockade breakdown phenomenology We continued to explore the photon blockade breakdown in a continuously driven cavity QED system, a prime example of a first-order driven-dissipative quantum phase transition, in a collaboration with the Quantum Integrated Devices Laboratory at the Institute for Science and Technology, Austria. By coupling a single transmon qubit to a superconducting cavity with an in situ tunable bandwidth, we observed the system transitioning from microscopic behavior dominated by quantum fluctuations to increasingly macroscopic behavior, characterized by stable phases and long timescale switching between coherent and vacuum states. Our findings, supported by neoclassical theory and quantum-jump Monte Carlo simulations, revealed the potential of such systems for quantum sensing and metrology. We introduced a superquantization rule that identifies robust stationary states in driven-dissipative systems, confirming its accuracy through numerical simulations and demonstrating the resilience of multistability in a cavity-qudit system to single-emitter decay. Additionally, we examined the photon-blockade breakdown bistability through a comparative analysis of fully quantum, semiclassical, and neoclassical models. We demonstrated the robustness of the neoclassical description, rooted in the high quantum purity of the bright state, which distinguishes this phenomenon from conventional optical bistability.

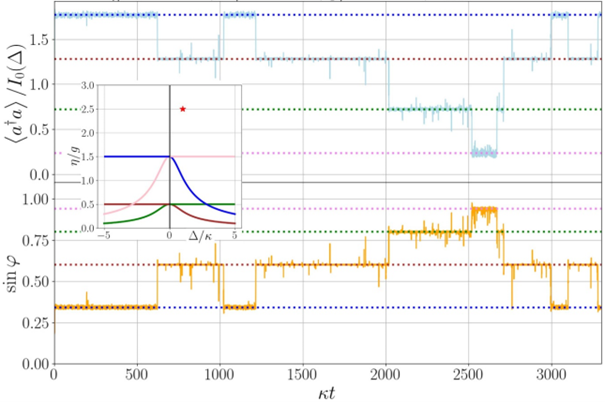
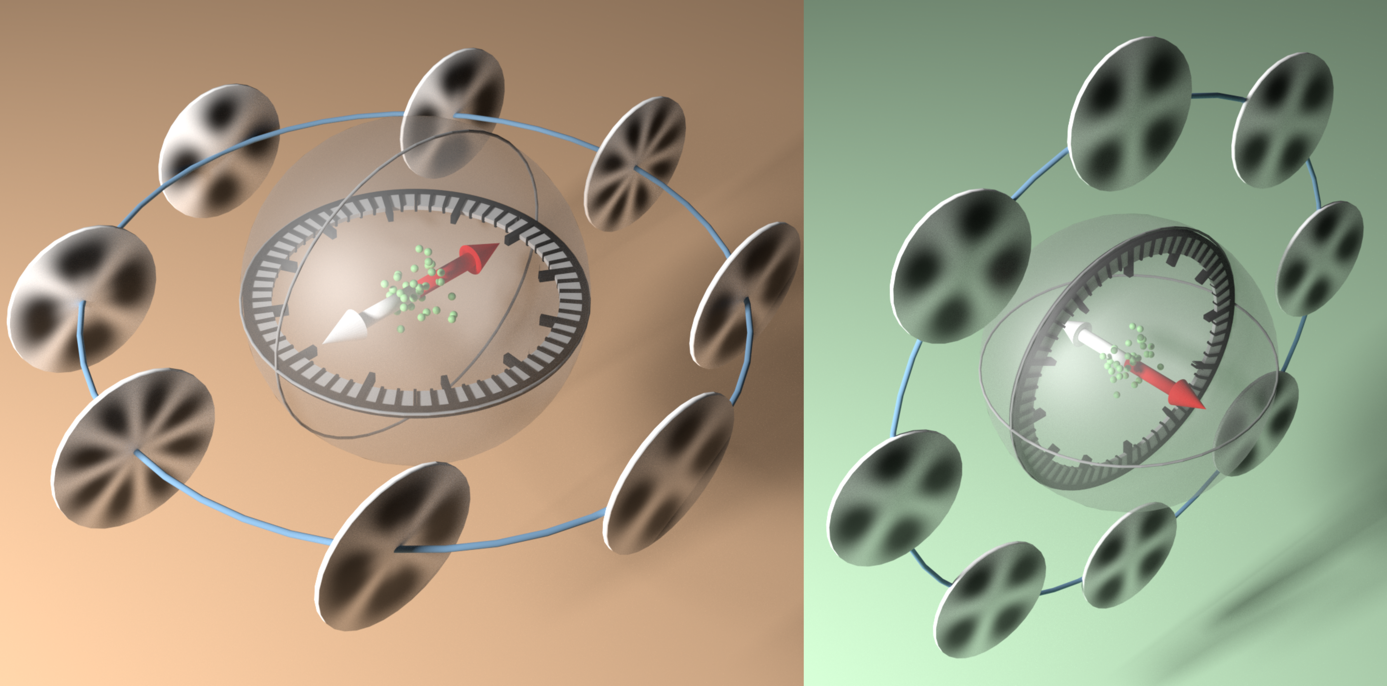
 Figure 3. Quantum trajectory simulations of cavity output exhibiting multistability.

References
Sett, Riya, Farid Hassani, Duc Phan, Shabir Barzanjeh, Andras Vukics, and Johannes M. Fink. "Emergent macroscopic bistability induced by a single superconducting qubit." PRX Quantum 5, no. 1 (2024): 010327. 
Német, Nikolett, Árpád Kurkó, András Vukics, and Péter Domokos. "Superquantization rule for multistability in driven-dissipative quantum systems." New Journal of Physics 26 (2024): 093009.
Kurkó, Árpád, Nikolett Német, and András Vukics. "How is photon-blockade breakdown different from optical bistability? A neoclassical story." JOSA B 41, no. 8 (2024): C29-C37.
 

2023

Experiment on Cavity Quantum Electrodynamics with cold Rb atoms. — We experimentally demonstrated an optical bistability between two hyperfine atomic ground states, using a single mode of an optical resonator in the collective strong coupling regime. Whereas in the familiar case, the bistable region is created through atomic saturation, we found an effect between states of high quantum purity, which is essential for future information storage. The nonlinearity of the transitions arise from cavity-assisted pumping between ground states of cold, trapped atoms and the stability depends on the intensity of two driving lasers. We interpret the phenomenon in terms of the recent paradigm of first-order, driven-dissipative phase transitions, where the transmitted and driving fields are understood as the order and control parameters, respectively. A semiclassical mean-field theory is invoked to underly the non-trivial two-dimensional phase diagram arising from the competition of the two drive. The saturation-induced bistability is recovered for infinite drive in one of the controls. The order of the transition is confirmed experimentally by hysteresis in the order parameter when either of the two control parameters is swept repeatedly across the bistability region.
  

Figure 1. Ground-state bistability of atoms in the cavity controlled by the power ratio of two drive lasers.  (a) The configuration of our CQED scheme. Cold atoms are loaded into a linear cavity and kept in a magnetic quadrupole trap. The cavity is driven with variable effective amplitude η through an incoupling mirror and the transmitted light detected with an avalanche photodiode. The atoms are illuminated from the side by a repump laser of variable power, characterized by the pumping rate λ. (b) The relevant part of the atomic level scheme. The transition from the ground state |g⟩to the excited state |e⟩ couples to the cavity mode, resulting in an effective drive amplitude, gα, where α is the field mode amplitude. The transversely injected repump laser drives the transition from |f ⟩ to |g ⟩ via other excited states (not indicated). Panels show the cavity transmission accompanying the optical pumping into the |f⟩ to |g⟩. (c) Atoms in state |g⟩ detune the cavity mode resonance with respect to the laser frequency set on resonance with the empty cavity.

Reference
B Gábor, D Nagy, A Dombi, TW Clark, FIB Williams, KV Adwaith, A Vukics, P Domokos, Ground-state bistability of cold atoms in a cavity, 
Phys. Rev. A 107, 023713 (2023) 

Theory of quantum phase transitions. - First-order phase transitions are ubiquitous in nature; however, this notion is ambiguous and highly debated in the case of open quantum systems. We constructed a paradigmatic example which allows for elucidating the key concepts. We showed that atoms in an optical cavity can manifest a first-order dissipative phase transition where the stable coexisting phases are quantum states with high quantum purity. These states include atomic hyperfine ground states and coherent states of electromagnetic field modes. The scheme benefits from the collective enhancement of the coupling between the atoms and the cavity field. Thereby we proposed a readily feasible experimental scheme to study the dissipative phase transition phenomenology in the quantum limit, allowing for, in particular, performing a finite-size scaling to the thermodynamic limit. 

Figure 2. (left) Scheme of ground-state bistability: ensemble of cold atoms interact with two driven modes which excite different hyperfine ground states. (right) Phase diagram with domains with different number of stable solutions of the system (1) on the plane of the drive amplitudes η₁, n₂. The cooperativity increases from (a) to (d), corresponding to atom numbers N = 5 10³, 10⁴, 10⁵, and 10⁶, respectively, with the single atom coupling g(N = 1) = 0.1γ. Ground-state bistability takes place in the low excitation limit, i.e., along the small white arcs (η₁²+η₂²=const.) in the bottom left corner of the panels, where the single-valued solution domain (blue) changes to bistability (purple) in a finite range of the ratio η₁/ η₂.

Reference
B. Gábor, D. Nagy, A. Vukics, and P. Domokos, Quantum bistability in the hyperfine ground state of atoms,  Physical Review Research 5, L042038 (2023) 

2022

Experiment on Cavity Quantum Electrodynamics with cold Rb atoms. — We discovered a dynamical, multi-level atom-cavity blockade effect and monitor its breakdown transition in time. As in the case of optical bistability, atoms initially impede transmission by detuning a cavity mode from the driving laser. The interacting system however, eventually transitions into an uncoupled state via a critical run-away process: resulting in maximum transmission. These two extremes of transmission are macroscopic reflections of well-defined atomic states, and thus are interpreted as phases of a dynamical transition. By monitoring the output of the cavity, we make time-resolved measurements of the order parameter and that of the enhanced photon number fluctuations. Considering these results for different cavity driving intensities, we establish finite-size scaling relations that suggest such a runaway effect is in fact a genuine dynamical phase transition.
 

Figure 1. Transmission-blockade-breakdown phase transition of atoms in the cavity.  Atoms can be in  `red' (disk), (a), or `green' (filled), (c),  states, blocking or permitting the light transmission through the cavity, respectively. In the transition domain, (b), the atoms are in a mixture of red (disk) and green (filled) states. Upper level schemes show the cavity mode frequency with respect to the angular frequency of the pump laser, w and in panel (d), red (disk) and green (filled) states are identified with the hyperfine states of 87Rb (only a part of the 5²S_1/2 ↔ 5²P_3/2structure is shown). Far-off-resonance σ^--polarized light provides an excitation path that assists the atoms' escape from the blockading state to the F=1 manifold of the electronic ground state. Atoms are first weakly excited to an intermediary state, (F, m_F) =( 2, 1), before spontaneously decaying to the manifold, which is optically dark with respect to the cavity mode. The time evolution of the transmitted intensity is plotted in (e), exhibiting the switch from blockaded to transparent phase around 100 ms after turning on the cavity drive. It is expressed in units of cavity photon number deduced from the detected photon flux. The transition is accompanied by the increase in cavity field fluctuations, represented in (f), in terms of thermal photon numbers extracted from the displaced, thermal-state statistics of the transmitted light.

Reference
T. W. Clark, A. Dombi, F. I. B. Williams, Á. Kurkó, J. Fortágh, D. Nagy, A. Vukics, P. Domokos, Time-resolved observation of a dynamical phase transition with atoms in a cavityPhys. Rev. A 105, 063712 (2022)

Microwave-optical conversion. - Stimulated Raman scattering on  atoms is a promising tool for generating optical photons from a microwave excitation in the ground-state hyperfine manifold. We consider an atomic Bose-Einstein condensate coupled to a microwave field that scatters photons into the guided modes of a nearby optical fiber. Due to momentum transfer to the condensate, stimulated photon scattering can occur outside of the phase-matched direction, which can be used to separate the converted photons from the strong Raman readout pulse. Conversely, in the phase-matched direction, superradiant scattering due to bosonic enhancement leads to an increased collection efficiency in the guided modes of the fiber, for which we determine optimal conditions.

Figure 1. (left) The geometry of the system of atoms, paraxial optics, and the fiber. (Right) The relevant atomic states and excitation paths.

Reference
Árpád Kurkó, Peter Domokos, David Petrosyan, and András Vukics, Collection efficiency of optical photons generated from microwave excitations of a Bose-Einstein condensate, Phys. Rev. A 105, 053708 (2022)

2021

Experiment on Cavity Quantum Electrodynamics with cold Rb atoms. — We developed our cavity QED experimental setup. We studied experimentally the optical dipole trapping of a cloud of cold atoms in a high-finesse cavity in the parameter regime where the atomic back-action on the cavity mode is significant. Back-action based effects lead to state selective optical manipulation schemes.  We identify a parameter range where the collective back action of the atoms is needed for the trapping, i.e., a single atom would not be trapped under the same laser drive conditions. The collective self-trapping is demonstrated by the observation of a significant increase of the trapping time as a function of the atom number. The atomic back action on the cavity field gives rise to a simultaneous real-time monitoring of the number of trapped atoms. This is used to show a non-exponential collapse of the atom trap.     
 

Figure 1. Self-trapping of atoms in the cavity.  Time evolution of the cavity output power with 5 $\mu$s resolution, averaging over ten realizations. The trajectory reveals an enhanced transmission when the trapped atoms bring the mode closer to resonance with the external drive field. This field entering the cavity provides for the optical dipole trap for the atoms.
 

Figure 2. Demonstration of the collective effect in the trapping. The trapping time depends on the number of atoms loaded into the cavity mode.

Reference:
A. Dombi, T. W. Clark, F.I. B. Williams, F. Jessen, J. Fortágh, D. Nagy, A. Vukics, P. Domokos: Collective self-trapping of atoms in a cavity, New J. Phys. 23 083036 (2021)
link to: https://iopscience.iop.org/article/10.1088/1367-2630/ac1a3c/pdf

Imaging of cold atoms. - We described and demonstrated how 3D magnetic field alignment can be inferred from single absorption images of an atomic cloud. While optically pumped magnetometers conventionally rely on temporal measurement of the Larmor precession of atomic dipoles, here a cold atomic vapor provides a spatial interface between vector light and external magnetic fields. Using a vector vortex beam, we inscribed structured atomic spin polarization in a cloud of cold rubidium atoms and recorded images of the resulting absorption patterns. The polar and azimuthal angles of an external magnetic field can then be deduced with spatial Fourier analysis. This effect presents an alternative concept for detecting magnetic vector fields and demonstrates, more generally, how introducing spatial phases between atomic energy levels can translate transient effects to the spatial domain.

Figure 3. Schematic representation of the measurement of magnetic field alignment from Fourier analysis of the atomic absorption profiles.

Reference:
1. F Castellucci, TW Clark, A Selyem, J Wang, S Franke-Arnold
Atomic Compass: Detecting 3D Magnetic Field Alignment with Vector Vortex Light,
Physical Review Letters 127 (23), 233202 (2021) Link to: https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.127.233202

Nonrelativistic quantum electrodynamics. - We showed that the Power–Zienau–Woolley picture of the electrodynamics of nonrelativistic neutral particles (atoms) can be derived from a gauge-invariant Lagrangian without making reference to any gauge whatsoever in the process. This equivalence is independent of choices of canonical field momentum or quantization strategies. In the process, we emphasize that in nonrelativistic (quantum) electrodynamics, the always appropriate generalized coordinate for the field is the transverse part of the vector potential, which is itself gauge invariant, and the use of which we recommend regardless of the choice of gauge, since in this way it is possible to sidestep most issues of constraints. Furthermore, we pointed out a freedom of choice for the conjugate momenta in the respective pictures, the conventional choices being appropriate in the sense that they reduce the set of system constraints.

Reference:
A. Vukics, G. Kónya, P. Domokos
The gauge-invariant Lagrangian, the Power–Zienau–Woolley picture, and the choices of field momenta in nonrelativistic quantum electrodynamics
Scientific Reports 11, 16337 (2021)
Link to: https://www.nature.com/articles/s41598-021-94405-z

2020

Experiment on Cavity Quantum Electrodynamics with cold Rb atoms. — We developed further our cavity QED experimental setup and achieved the detection of atoms within the resonator. We performed the first measurements with cold trapped Rb atoms interacting with the mode of a high finesse optical resonator. We studied the photo-electron statistics of the probe light transmitted through the resonator for different configuration of the atom cloud in the mode.      
 

Figure 1. First observation of atoms in the cavity.  The time evolution of the transmitted intensity of an optical resonator is plotted for various frequency detunings between the probe laser light and the resonator mode. The peaks describe the effect of the atoms on the transmission. The sign of the change (peak vs. dip) is in good agreement with the theoretically expected effect. For negative detuning between the laser and the resonator, the atoms shift the resonance mode frequency closer to that of the laser, therefore the transmission exhibits peaks, as can be seen in the upper row. The measured data allow for a calibration of various parameters of the system, e.g., the atom number in the cavity.

Cavity Quantum Electrodynamics with Bose-Einstein condensates. — The interaction of a magnetically trapped Bose–Einstein condensate of Rubidium atoms with the stationary microwave radiation field sustained by a coplanar waveguide resonator (CPW) has been studied. This coupling allows for the measurement of the magnetic field of the resonator by means of counting the atoms that fall out of the condensate due to hyperfine transitions to non-trapped states. We determined the quantum efficiency of this detection scheme and showed that weak microwave fields at the single-photon level can be sensed.

Figure 2. Detection efficiency of the magnetically levitated BEC in sensing microwave photons of a coplanar resonator. The ultracold atom cloud is situated at the center of the central conductor of the coplanar waveguide resonator. The geometry of the CPW ensures that its magnetic field is polarized in the x direction at the location of the BEC. The magnetic field Bx (t) of the CPW oscillates in time with an angular frequency which is resonant with a magnetic dipole transition of the BEC atoms, and induces transitions from the trapped state into an untrapped one. A one-photon microwave field in the resonator generates an atom current of about 3 atoms per 1.7 millisecond.

References:
[1] O. Kálmán and P. Domokos, EPJ Quantum Technology (2020) 7:2

2019

Experiment on Cavity Quantum Electrodynamics with cold Rb atoms. ― We set up a single mode optical cavity in the UHV chamber and frequency stabilized one of the fundamental modes (4 MHz linewidth) to the Rubidium 780 nm D2 transition line by piezo feedback and by means of the Ponder-Drever-Hall (PDH) method. We created a magneto-optical trap and Rb captured atoms from vapour. The fluorescence of the trapped atom cloud is shown in Fig. 1. We developed the absorption imaging technique to determine the number of atoms (~10⁸) and the temperature in the trap, which, after polarisation gradient cooling, is about 100 microKelvin. The atoms, optically pumped to a well defined magnetic state, have been loaded into a purely magnetic trap which allows for transporting the atoms, eventually to position them into the volume of the optical cavity. The system is close to realise the atom-photon interface for the first set of planned experiments.

Figure 1. Adiabatic transport of cold Rb atoms in the magnetic trap into the optical cavity. 

Cavity Quantum Electrodynamics, quantum critical phenomena. ― We completed and justified the interpretation of the photon-blockade-breakdown effect as a first-order dissipative quantum phase transition. To this end, we introduced the concepts of thermodynamic limit and finite-size scaling for the microscopic system of a driven dissipative Jaynes-Cummings model. The thermodynamic limit is  defined for this microscopic system in such a way that the number of relevant degrees of freedom remains fixed. Instead of growing the system size, the scaling of the parameters keeps the form of the stationary solution of the driven-dissipative system invariant. At the same time, the proposed finite-size scaling leads to an increasing robustness of the attractor states associated with the bistability signal, until these states reach full stability in the thermodynamic limit. On approaching this limit, at variance with the fluorescence shelving experiment, no single quantum jump or other microscopic event can flip the system from one phase to the other. In the thermodynamic limit, the blinking telegraph-like signal vanishes completely and the state of the system is determined by the initial condition, similarly to the usual hysteresis behaviour in classical critical systems. If such a finite size scaling is possible – and here we show that this is the case for the photon-blockade breakdown effect –, then the bistability that can be observed in a given experimental realization of the system with its finite parameters not in the thermodynamic limit, can be considered the finite-size approximation of what is a genuine first-order phase transition in the thermodynamic limit.

Figure 2. Classical phase diagram of the driven Jaynes-Cumings model in the ultrastrong coupling regime. The photon-blockade-breakdown phase transition can be induced by changing the drive amplitude (vertical axis) or the drive frequency (horizontal axis). We studied the finite-size scaling in the vicinity of the blue star, which is in the middle of the bistability region.

Numerical methods in Quantum Optics. —  We developed a stepwise adaptive-timestep version of the Quantum Jump (Monte Carlo wave-function) algorithm. Our method has proved to remain robust even for problems where the integrating implementation of the Quantum Jump method is numerically problematic. The only specific parameter of our algorithm is the single a priory parameter of the Quantum Jump method, the maximal allowed total jump probability per timestep. We studied the convergence of ensembles of trajectories to the solution of the full master equation as a function of this parameter. This study is expected to pertain to any possible implementation of the Quantum Jump method.

External links:

[1] Vukics, Dombi, Fink, Domokos, Quantum 3, 150 (2019)
[2] Kornyik, Vukics, Computer Physics Communications 238, 88-101 (2019)
 

2018

Experiment on Cavity Quantum Electrodynamics with cold Rb atoms ― We set up a new laboratory for cavity QED experiments with ultracold Rb atoms. We realized the UHV system which is operated in the pressure range below 1e-10 mbar, and includes the magneto-optical trap and the in-vacuo high-finesse single-mode optical resonator.  We completed the optical system which is based on three laser sources that are referenced to   Rb resonance line by Doppler-free non-linear spectroscopy. By means of acousto-optical modulators we provide the narrow linewidth phase-locked laser sources at five different frequencies for atomic manipulation.
 

Fig. 1. Photo of the actual status of the cavity QED laboratory.

Cavity Quantum Electrodynamics, quantum critical phenomena. ― The quantum measurement back action noise effects on the dynamics of an atomic Bose lattice gas inside an optical resonator has been described by means of a hybrid model consisting of a Bose–Hubbard Hamiltonian for the atoms and a Heisenberg–Langevin equation for the lossy cavity field mode. Considering atoms initially being prepared in the ground state of the lattice Hamiltonian, we calculated the transient dynamics due to the interaction with the cavity mode. We showed that the cavity field fluctuations originating from the dissipative outcoupling of photons from the resonator lead to vastly different effects in the different possible ground state phases, i.e., the superfluid, the supersolid, the Mott- and the charge-density-wave phases. In the former two phases with the presence of a superfluid wavefunction, the quantum measurement noise appears as a driving term leading to depletion of the ground state. The time scale for the system to leave the ground state was presented in a simple analytical form. For the latter two incompressible phases, the quantum noise results in the fluctuation of the chemical potential. We derived an analytical expression for the corresponding broadening of the quasiparticle resonances.  [Phys. Rev. A 97, 063602 (2018) ]
 

Fig. 2. Illustration of the coupled cavity Bose-Hubbard model setup. An atomic cloud is loaded into a square optical lattice, which is inside a single-mode high-Q Fabry-Pérot resonator. The period of the cavity mode is approximately equal to that of the optical lattice. The cavity is pumped from the side by light scattering off the atoms. The system is open,  together with the external drive, the photons leak out from the cavity, resulting in heating and decoherence, or, in other terms, quantum measurement back action since the out coupled photons can be measured by classical detectors.

Ultracold gases, Bose-Einstein condensates. ― We studied quasiparticle scattering effects on the dynamics of a homogeneous Bose-Einstein condensate of ultracold atoms coupled to a single mode of an optical cavity. The relevant excitations, which are polariton-like mixed excitations of photonic and atomic density-wave modes, have been identified. All the first-order correlation functions were presented by means of the Keldysh Green’s function technique. Beyond confirming the existence of the resonant enhancement of Beliaev damping, we found a very structured spectrum of fluctuations. There is a spectral hole burning at half of the recoil frequency reflecting the singularity of the Beliaev scattering process. The effects of the photon-loss dissipation channel and that of the Beliaev damping due to atom-atom collisions could have been well separated. We showed that the Beliaev process does not influence the properties of the self-organization criticality. [Phys. Rev. A 98, 063608 (2018)]

(a)

(b)

FIG. 3 (a) The schematic picture of an atomic ensemble inside a Fabry-Pérot cavity is pumped from the side by a laser close to resonance with the cavity. The atomic gas undergoes self-organization for strong enough laser drive: the atoms scatter photons from the laser to the cavity and may create a classical field serving as an optical lattice trapping them even further in the optimal scattering positions. (b) Spectrum of the quasiparticle excitation. Large detuning ∆C = 100 implies little mixing of the condensate quasiparticle with the photon mode. The enhanced Beliaev scattering process is manifested by the large peak, which exhibits a hole burning at 0.5. (All angular frequencies are expressed in units of the recoil frequency.) The correlation function is plotted for different coupling strengths y approaching the critical value yc: y = 0 (solid red), y/yc = 0.5 (short-dashed green), 0.7 (dotted blue), 0.8 (dashed-dotted orange), 0.9 (dashed-double-dotted brown), 0.95 (long-dashed magenta). 

We studied the spin-1 bilinear–biquadratic model on the complete graph of N sites, i.e. when each spin is interacting with every other spin with the same strength. Because of its complete permutation invariance, this Hamiltonian can be rewritten as the linear combination of the quadratic Casimir operators of SU(3) and SU(2). Using group representation theory, we explicitly diagonalized the Hamiltonian and mapped out the ground-state phase diagram of the model. Furthermore, the complete energy spectrum, with degeneracies, was obtained analytically for any number of sites. [J. Phys. A: Math. Theor. 51, 105201 (2018) ]
 

2017

Cavity Quantum Electrodynamics, quantum critical phenomena. ― Non-equilibrium phase transitions exist in damped-driven open quantum systems, when the continuous tuning of an external parameter leads to a transition between two robust steady states.

In second-order transitions, this change is abrupt at a critical point, whereas in first-order transitions, the two phases can co-exist in a critical hysteresis domain. In collaboration with the experimental group of the ETH Zürich, we found a first-order dissipative quantum phase transition in a driven-circuit quantum electrodynamics (QED) system. It takes place when the photon blockade of the driven cavity-atom system is broken by increasing the drive power. The observed experimental signature is a bimodal phase space distribution with varying weights controlled by the drive strength. The measurements showed an improved stabilization of the classical attractors up to the millisecond range when the size of the quantum system is increased from one to three artificial atoms. The theoretical work included the fitting of the experimental data as well as it contributed to prove the phase-transition character of the effect. Furthermore it was possible to prove theoretically that the photon-blockade-breakdown effect relies on a given range of the parameters of a three-level atomic system. We showed that the parameters of the actual experimental setup happen to correspond to this range.

Ultracold gases, Bose-Einstein condensates. ― Modeling the coupling between a trapped Bose-Einstein condensate and a current carrying nanowire, we studied, in collaboration with an experimental group at Tübingen, the magneto-mechanical interaction by means of classical radio-frequency sources.  We performed the spectral analysis and the local measurement of intensity correlations of microwave fields using ultracold quantum gases. The fluctuations of the electromagnetic field induce spin flips in a magnetically trapped quantum gas and generate a multimode atom laser. The output of the atom laser was measured with high temporal resolution on the single-atom level, from which the spectrum and intensity correlations of the generating microwave field have been reconstructed in accordance with our recently proposed scheme. We gave the theoretical description of the atom-laser output and its correlations in response to resonant microwave fields and verified the model with measurements on an atom chip. The measurement technique is applicable for the local analysis of classical and quantum noise of electromagnetic fields, for example, on chips, in the vicinity of quantum electronic circuits.

Figure 1. (a) Simulated histogram of the output intensity as a function of the coupling constant g2 between the two excited atomic states |eñ and |fñ at a given driving amplitude h with red representing high probability and blue indicating zero probablility. This plot shows that only a certain range of the ratio g2/g1 gives rise to bistability.

(b) Measured vacuum Rabi spectra for various input powers with all three atoms in resonance with the cavity. For better visibility the shown spectra are offset by 1.6 nW from each other. The sharp transmission peak shown in the inset appears stochastically. In this particular measurement (orange line at 4.4 fW input power), we observe only two frequency points with small but finite switching probability and we sample over multiple switching events resulting in a certain mean detected power. At lower drive power, no transmission is observed (no switching). At higher drive powers, the transmission peak approaches the cavity linewidth and scales linearly with input power (no switching again).

(c) Measured histogram of the detected power as a function of the cavity input power for a single transmon (density plot). The most likely photon numbers (line plots) are extracted from this measurement (red) and two similar measurements taken with 2 (orange) and 3 qubits (green) in resonance with the cavity mode. Simulation results for the single qubit case are shown with connected black symbols for comparison. The dashed line is for reference and represents the response of the empty cavity.

Figure 2. (a) Cold-atom spectrometer (not to scale) consisting of a magnetically trapped Bose-Einstein condensate and an ionization-based single-atom detector. (b) The microwave couples atoms at resonance surfaces given by equipotential surfaces of the atomic Zeeman potential, i.e., magnetic isofield lines (dashed lines). Due to gravity, the BEC is displaced from the magnetic trap center and the resonance surfaces become nearly plane. Without amplitude modulation, the microwave carrier couples atoms from a single resonance surface (red solid thick line) with a position given via ωc. Amplitude modulation at a single frequency generates sidebands to the carrier and outcoupling from two resonance surfaces (green solid thin lines). (c) Normalized spectral response γ(ω)/γmax of a BEC to a single microwave frequency (black dots) and model function (red line).

2016

Cavity Quantum Electrodynamics, quantum critical phenomena ― Quantum phase transitions in driven-dissipative systems opened up a novel research area in the field of critical phenomena. These transitions lie beyond the standard classification of dynamical or equilibrium phase transitions, and define completely new universality classes.  In an open quantum system, the critical behaviour appears in the state formed by the dynamical equilibrium of the external driving and dissipation processes. The abrupt symmetry breaking change of such a steady state takes place when the external control parameters are continuously tuned across the critical point. The correlation functions at the critical point are determined by non-equilibrium noise rather than thermal or ground-state quantum fluctuations. We demonstrated that criticality in a driven-dissipative system is strongly influenced by the spectral properties of the bath. We studied the open-system realization of the Dicke model, where a bosonic cavity mode couples to a fictious large spin formed by two motional modes of an atomic Bose-Einstein condensate. The cavity mode is driven by a high-frequency laser and it decays to a Markovian bath, while the atomic mode interacts with a colored bath. We revealed that the soft mode fails to describe the characteristics of the criticality. We calculated the critical exponent of the superradiant phase transition and identified an inherent relation to the low-frequency spectral density function of the colored bath. We showed that a finite temperature of the colored bath does not modify qualitatively this dependence on the spectral density function.

We investigated the possibility of the Dicke-type superradiant phase transition of an atomic gas. We described the ultrastrong coupling limit of the interaction between light and atoms within the regularized electric dipole gauge, in which we can take into account the short-range depolarizing interactions between atoms that approach each other as close as the atomic size scale. By using a mean field model, we find that a critical point does indeed exist, though the atom-atom contact interaction shifts it to a higher value than what can be obtained from the bare Dicke-model. We pointed out the proximity of the critical density to that of solidification, which leads to the conjecture that the system, at the critical density, goes over to the condensed rather than to the “superradiant” phase.

Ultracold gases, Bose-Einstein condensates ― Bose-Einstein condensates of ultracold atoms can be used to sense fluctuations of the magnetic field by means of transitions into untrapped hyperfine states. It has been shown recently that counting the outcoupled atoms can yield the power spectrum of the magnetic noise. As a continuation of our previous investigations, we calculated the spectral resolution function, which characterizes the condensate as a noise measurement device in this scheme. We used the description of the radio-frequency outcoupling scheme of an atom laser, which takes into account the gravitational acceleration. Employing both an intuitive and the exact three-dimensional and fully quantum mechanical approach, we derived the position-dependent spectral resolution function for condensates of different size and shape.

We investigated the magnetic properties of strongly interacting four-component spin-3/2 ultracold fermionic atoms in the Mott insulator limit with one particle per site in an optical lattice with honeycomb symmetry. In this limit, atomic tunneling is virtual, and only the atomic spins can exchange. We found a competition between symmetry-breaking and liquid-like disordered phases. Particularly interesting are the non-singlet valence bond states (where the valence bonds have non-zero magnetization) which are situated between the ferromagnetic and conventional valence bond phases. In the framework of a mean-field theory, we calculated the phase diagram and identified an experimentally relevant parameter region where a homogeneous SU(4) symmetric Affleck-Kennedy-Lieb-Tasaki–like valence bond state is present.

The classical ground states of the SU(4) Heisenberg model on the face-centered-cubic lattice constitute a highly degenerate manifold. We explicitly constructed all the classical ground states of the model. To describe quantum fluctuations above these classical states, we applied linear flavor-wave theory. At zero temperature, the bosonic flavor waves select the simplest of these SU(4) symmetry-breaking states, the four-sublattice-ordered state defined by the cubic unit cell of the fcc lattice. Due to geometrical constraints, flavor waves interact along specific planes only, thus rendering the system effectively two dimensional and forbidding ordering at finite temperatures. We showed that longer-range interactions generated by quantum fluctuations can shift the transition to finite temperatures.