Kvantuminformatika és a Komplex Rendszerek Kutatócsoport

2023

Quantum annealing with heterogeneous fields. — In transverse-field Ising models, disorder in the couplings gives rise to an unfavorable, slower-than-algebraic scaling of the density of defects produced when the system is driven through its quantum critical point. By applying Kibble-Zurek theory and numerical calculations, we demonstrated in the one-dimensional model that the scaling of defect density with annealing time can be made algebraic by balancing the coupling disorder with suitably chosen inhomogeneous driving fields. We also studied defect production during an environment-temperature quench of the open variant of the model in which the system is slowly cooled down to its quantum critical point. According to our results, uncorrelated disorder induces a logarithmic temporal decrease of the defect density, while balanced disorder leads again to an algebraic decay [1].

Renormalization theory of disordered contact processes. — Motivated by long-range dispersal in ecological systems, we formulated and applied a general strong-disorder renormalization group framework to describe one-dimensional disordered contact processes with heavy-tailed (such as power law, stretched exponential, and log-normal) dispersal kernels, widely used in ecology. The focus was on the close-to-critical scaling of the order parameters, including the commonly used density, as well as the less known persistence. Our results reveal that the more slowly decaying dispersal kernels lead to faster-vanishing densities as the critical point is approached. The persistence, however, shows an opposite tendency: the broadening of the dispersal makes its decline sharper at the critical point [2]. 

Correcting coherent and readout errors in the surface code. — Quantum Error Correction is a crucial component of large-scale quantum computation, the only way to achieve the low error rates required for precise algorithms. The surface code is the currently leading quantum error correction protocol, which has recently been implemented on various quantum computer prototypes. Although it is thoroughly understood how the surface code offers protection of quantum data against incoherent (random Pauli) errors, the level of protection it ensures against coherent errors is less well known. We tested numerically the performance of the surface code against a combination of coherent and readout errors, using a recently developed simulation approach (mapping the quantum state of the processor to a multifermion system). We found that there is an error correction threshold here, with a value close to that of the corresponding incoherent error channel [3]. 

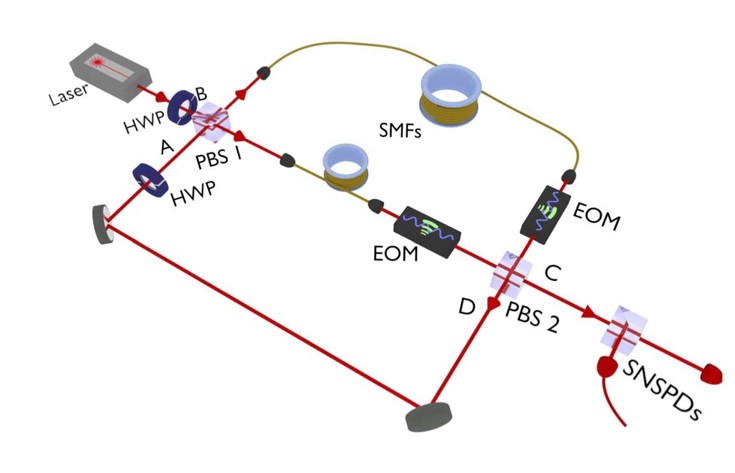
Sequential unsharp measurement of photon polarization. – We propose a general experimental scheme based on binary trees of partially polarizing beam splitters (PPBSs) for realizing sequential unsharp measurements of photon polarization. The sharpnesses and the bases of the particular photon polarization measurements can be chosen arbitrarily by using corresponding PPBSs and phase plates in the setup. In the limit of low sharpnesses the scheme can realize sequential weak measurements, too. We develop a general formalism for describing sequential unsharp measurements of photon polarization in which the particular unsharp measurements are characterized by appropriate measurement operators. We show that a straightforward experimental realization of this model is the proposed scheme. In this formalism the output polarization states after the sequential measurement and any correlation functions  characterizing the measurement results can be easily calculated. Our model can be used for analyzing the consequences of applying postselection and reselection in the measurement. We derive the anomalous mean value for an unsharp polarization measurement with postselection and the anomalous second-order correlation function for the sequential unsharp measurement of photon polarization with reselection. We show that these anomalies can be easily measured using the proposed scheme. [4]

Multiplexed single-photon sources with optimal structure. – We consider novel types of spatially multiplexed single-photon sources based on output-extended incomplete binary-tree multiplexers containing general asymmetric routers where the construction of the multiplexers takes into account the total transmission efficiencies of the multiplexer arms at which a novel router can be added to the system. After selecting the multiplexer that outperforms the others, we identify the ranges of the loss parameters for which the application of the selected multiplexer leads to single-photon sources with higher single-photon probabilities and lower multiphoton noise than that can be achieved by using asymmetric multiplexers. We show that using the selected multiplexer is especially advantageous in the case of single-mode sources characterized by thermal statistics of the input photon pairs. We also reveal that the application of this multiplexer yields high performance single-photon sources even for suboptimal system sizes, which is a typical situation in current experiments. [5]

Entanglement in cold atoms. — We present a method to detect bipartite entanglement based on number-phase-like uncertainty relations in split spin ensembles. First, we derive an uncertainty relation that plays the role of a number-phase uncertainty for spin systems. It is important that the relation is given with well-defined and easily measurable quantities, and that it does not need assuming infinite dimensional systems. Based on this uncertainty relation, we show how to detect bipartite entanglement in an unpolarized Dicke state of many spin-1/2 particles. The particles are split into two subensembles, then collective angular momentum measurements are carried out locally on the two parts. First, we present a bipartite Einstein-Podolsky-Rosen (EPR) steering criterion. Then, we present an entanglement condition that can detect bipartite entanglement in such systems. We demonstrate the utility of the criteria by applying them to a recent experiment given in K. Lange et al. [Science 360, 416 (2018)] realizing a Dicke state in a Bose-Einstein condensate of cold atoms, in which the two subensembles were spatially separated from each other. Our methods also work well if split spin-squeezed states are considered. We show in a comprehensive way how to handle experimental imperfections, such as the nonzero particle number variance including the partition noise, and the fact that, while ideally BECs occupy a single spatial mode, in practice the population of other spatial modes cannot be fully suppressed. [6]

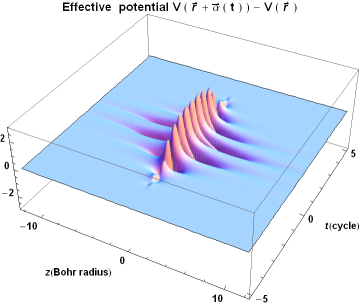
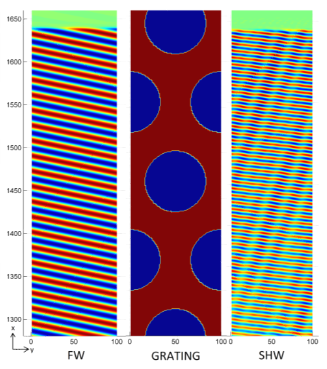
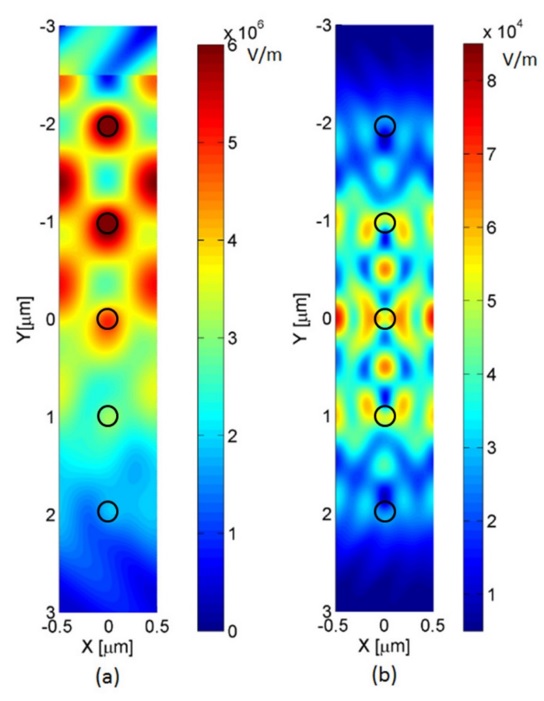
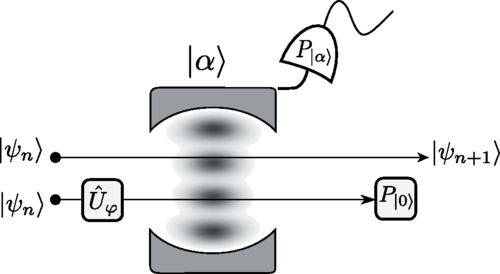
Propagating single photons from an open cavity. — We have derived and analyzed models for the system of an atom trapped in a cavity, featuring a semitransparent mirror and driven by laser pulses allowing the production of a single photon leaking out from the cavity. We introduced true-mode, inside-outside, and pseudomode representations for describing the system from first principles. From the exact modes of the system (the true-mode representation), we explicitly introduce the cavity-reservoir coupling, which allows one to describe the dynamics without any a priori approximations. We have demonstrated that under suitable approximations that we formulate, these different representations give accurate results that are similar to each other, yet generally differ. We particularly analyze a high-Q cavity scenario and show that this requirement alone, in general, is not enough for these approximate models to work. This is especially significant for the models where we consider cavities with higher losses and mode overlaps, namely, cavities with low refractive indices, such as plasmonic cavities. In nanophotonics, it is common to transpose these approximate models derived for optical cavities to plasmonic cavities. However, as shown here, these approximate models already yield different predictions for optical cavities with relatively high transmission. In the literature, it is common to phenomenologically introduce the pseudomode representation. However, this kind of phenomenological approach does not provide the full description of the produced photon, namely, the outgoing photon shape in the frequency domain. In contrast, here, we recover the phenomenological model derived from first principles; moreover, it is complemented with the complete description of the system, including the full characteristics of the photon in the time domain as well as in the frequency domain. This derivation justifies explicitly the Markov approximation producing an input-output relation from first principles via the nontrivial cavity-reservoir coupling. This allows a precise definition of the propagating outside photon state. Finally, concepts, such as the Poynting vector, photon flux, input-output operators, and photon state, that characterize the propagation of the resulting leaking photons have been defined and connected: We have formulated an input-output relation taking into account the propagating effects, which allows a direct interpretation of the out operator through the Poynting vector and the photon flux. The generated flux is then determined from the quantum average of the dynamics of the photon number in the cavity, which results from a standard master equation [7].

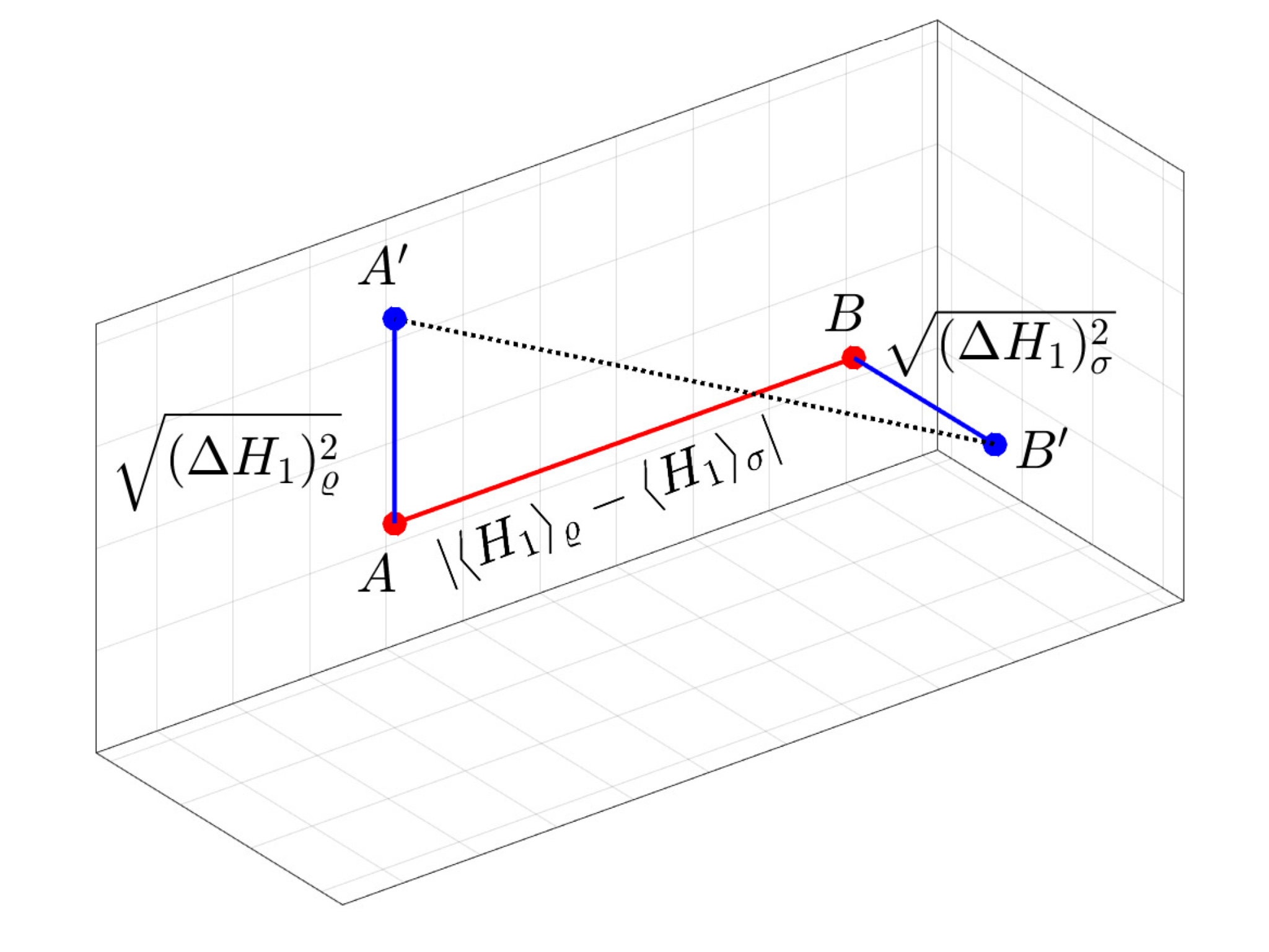
Quantum Optimal Transport. — In probability and statistics, defining the distance of probability measures or probability density functions plays a central role. However, many traditional distance definitions do not effectively characterize the difference between two density functions. For example, if two probability density functions p (x) and q(x) have disjoint support, that is, p(x)=0 whenever q(x)>0, at the usual distances p(x) and q(x) distance is maximal, regardless of how far the supports of p and q are from each other. Let e.g., p(x) is a function that is non-zero only for 0<x<1, while q(x) is non-zero only for 10<x<11. The distance will be maximal in the same way as if q(x) were non-zero only for 100<x<101. This phenomenon is usually expressed as the distance between p and q being insensitive to the underlying metric. The problem is remedied by the so-called Wasserstein distance defined in optimal transport theory, the basic idea of which can be illustrated with the following example. Suppose we have a pile of sand of a unit volume described by the density function p(x). We want to move this pile of sand to another place, and we expect it to have a density q(x). The transport is characterized by a cost function, which of course depends on the distance between the two piles of sand, i.e., the underlying metric. The Wasserstein distance is essentially the total cost of moving the sand from a pile with a distribution p(x) to another one with a distribution q(x). The Wasserstein distance can be defined in several ways for the quantum case. One of these possibilities is when the expected value of an operator is minimized on bipartite quantum states with a given marginal. A surprising feature of the so-called quantum Wasserstein-2 distance is that the self-distance, i.e., the distance of a quantum state from itself, can be non-zero. For the quantity defined by De Palma and Trevisan, the square of the self-distance is equal to the Wigner-Yanase skew information. In [8] Géza Tóth and József Pitrik showed that if we limit the optimization to the set of separable states, we get a new and interesting quantity. The paper examined the properties of the quantity and its relation to entanglement theory. They proved that the square of the self-distance is equal to the quantum Fisher information, a central notion in quantum metrology, over four, if we consider a single local operator to define the cost operator.

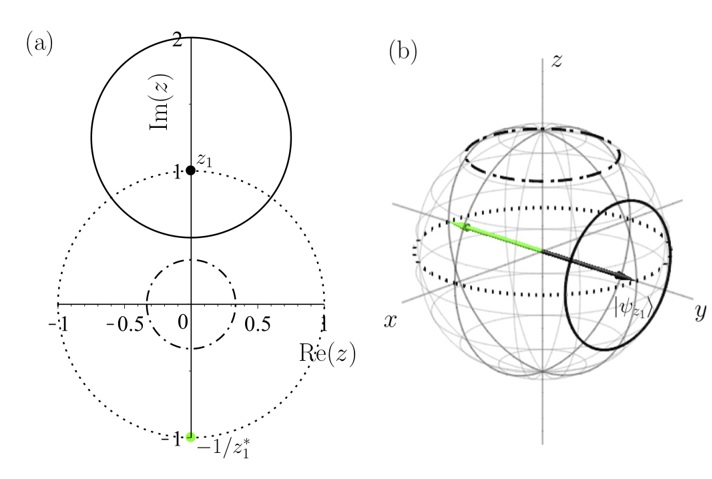
In the paper [9] the Wasserstein isometries of the quantum bit state space is described with respect to distinguished cost operators. A Wigner-type result is derived for the cost operator involving all the Pauli matrices: in this case, the isometry group consists of unitary or anti-unitary conjugations. In the Bloch sphere model this means that the isometry group coincides with the classical symmetry group O(3). On the other hand, for the cost generated by the qubit “clock” and “shift” operators, they discovered non-surjective and non-injective isometries as well, beyond the regular ones. This phenomenon mirrors certain surprising properties of the quantum Wasserstein distance.

References:

[1] R. Juhász, G. Roósz, Reducing defect production in random transverse-field Ising chains by inhomogeneous driving fields, Phys. Rev. B 108, 224203 (2023). https://doi.org/10.1103/PhysRevB.108.224203

[2] R. Juhász, Renormalization theory of disordered contact processes with heavy-tailed dispersal, Phys. Rev. Research 5, 033157 (2023). https://doi.org/10.1103/PhysRevResearch.5.033157

[3] Á. Márton, J.K. Asbóth, Coherent errors and readout errors in the surface code,    Quantum 7, 1116 (2023). https://doi.org/10.22331/q-2023-09-21-1116

[4] P. Adam, L. Diósi, Sequential unsharp measurement of photon polarization, Phys. Rev. A 107, 063706 (2023). https://doi.org/10.1103/PhysRevA.107.063706

[5] P. Adam, M. Mechler, Single-photon sources based on incomplete binary-tree multiplexers with optimal structure, Optics Express 31, 30194 (2023). https://doi.org/10.1364/OE.496206

[6] G. Vitagliano, M. Fadel, I. Apellaniz, M. Kleinmann, B. Lücke, C. Klempt, G. Tóth, Number-phase uncertainty relations and bipartite entanglement detection in spin ensembles, Quantum 7, 914 (2023). https://doi.org/10.22331/q-2023-02-09-914

[7] A. Saharyan, B. Rousseaux, Z. Kis, S. Stryzhenko, and S. Guérin, Propagating single photons from an open cavity: Description from universal quantization, Phys. Rev. Research 5, 33056 (2023). https://doi.org/10.1103/PhysRevResearch.5.033056

[8] G. Tóth, J. Pitrik, Quantum Wasserstein distance based on an optimization over separable states, Quantum 7, 1143 (2023). https://doi.org/10.22331/q-2023-10-16-1143

[9] G.P. Gehér, J. Pitrik, T. Titkos, D. Virosztek, Quantum Wasserstein isometries on the qubit state space, J. Math. Anal. Appl. 522, 126955 (2023). https://doi.org/10.1016/j.jmaa.2022.126955

2022

Nonlocal Boxes. — We have developed a Web Application Programming Interface (API) that is capable of implementing no-signaling correlations between pairs of parties [1,2]. Certainly it does not include particular measurements on entangled particles; the correlations are realized via communication with a central server. In this way, however, scenarios based on such correlations that involve quantum measurements and entanglement, like the Bell-CHSH experiment or device-independent quantum cryptographic protocols can be simulated using the API, making it a useful tool for protocol design and a basis for computer applications to help in experience-based teaching of nonclassical correlations. The development of the API has inspired our research resulting the first known two-party protocol in which using nonlocal boxes in different causal order is important [3]. Currently a mobile application to support the teaching of Bell-type scenarios is being developed.

Energy gap of transverse-field Ising chains. — Based on a relationship with continuous-time random walks discovered by Iglói, Turban, and Rieger, we derived exact lower and upper bounds on the lowest energy gap of open transverse-field Ising chains, which are explicit in the parameters and are generally valid for arbitrary sets of couplings and fields. Applying the bounds to a random Ising chain with coupling-field correlations, a model which is relevant for adiabatic quantum computing, we determined the critical dynamical exponent of the model and revealed the existence of logarithmic corrections at special points [4].

Wasserstein distance and quantum Fisher information. — A classical Wasserstein distance is a metric between probability distributions μ and ν, induced by the problem of optimal mass transportation. It reflects the minimal effort that is required in order to morph the mass of μ into the mass distribution of ν. Methods based on the theory of optimal transport and advantageous properties of Wasserstein metrics have achieved great success in several important fields of pure mathematics. The non-commutative generalization, the so-called quantum optimal transport, has been at the center of attention, as it led to the definition of several new and very useful notions in quantum physics. One of the key results of quantum optimal transport is the definition of the quantum Wasserstein distance. It has the often desirable feature that it is not necessarily maximal for two quantum states orthogonal to each other, which is beneficial, for instance, when performing learning on quantum data. Some of the properties of the new quantities are puzzling, yet point to profound relations between seemingly unrelated fields of quantum physics. For instance, the quantum Wasserstein distance order 2 of the quantum state from itself can be nonzero, while in the classical case the self-distance is always zero. In particular, the quantum Wasserstein distance has been defined based on a quantum channel formalism, and it has been shown that the square of the self-distance is equal to the Wigner-Yanase skew information of the quantum state. We obtained new quantities by restricting the optimization to separable states in the above definitions [5]. We showed that, in this case, the square of the self-distance equals the quantum Fisher information times a constant. The quantum Fisher information is a central quantity of quantum metrology, a field that is concerned with metrological tasks in which the quantumness of the system plays an essential role. This way we connected quantum optimal transport to quantum entanglement theory.

Figure 1. Geometric representation of the quantum Wasserstein distance between a pure state and a mixed state for operator H₁. The square of the distance is the sum of three terms of which two can be nonzero even if we calculate the distance of the state from itself, i.e, we calculate self-distance.

2021

Entanglement entropy scaling in random singlet states. — We considered random singlet phases of antiferromagnetic spin chains, in which the leading-order logarithmic divergence of the entanglement entropy, as well as the closely related leading term in the distribution of singlet lengths are well known by the strong-disorder renormalization group (SDRG) method. We addressed the question of how large the sub-leading terms of the above quantities are. By an analytical calculation performed along a special SDRG trajectory, we identified a series of integer powers of 1/l in the singlet-length distribution. This was confirmed by a numerical SDRG analysis which showed non-universal coefficients of the sub-leading term and also revealed terms with half-integer powers. We also presented how the singlet lengths originating in the SDRG approach can be interpreted and calculated in the XX chain from the one-particle states of the equivalent free-fermion model [1].

We considered a sublattice-symmetric free-fermion model on a one-dimensional lattice with random, power-law decaying hopping amplitudes, and addressed the question how far an analogue of the random-singlet state (RSS) is valid for this model. For this purpose, we studied the effective central charge characterizing the logarithmic divergence of the entanglement entropy (EE) and the prefactor of the distribution of distances between localization centers on the two sublattices, which must fulfill a consistency relation for a RSS. We found by exact diagonalization an overall logarithmic divergence of EE with an effective central charge varying with the decay exponent α of the hopping amplitudes. The consistency relation of RSS is violated for α≤2, while for α>2 it is possibly valid. The EE was also calculated by the SDRG method numerically. We constructed and applied an efficient minimal SDRG scheme, which turned out to be an accurate approximation of the traditional scheme [2].

Quantum optical description of high order multiphoton processes.— In the frame of nonrelativistic quantumelectrodynamics, we have constructed a general theoretical model for nonperturbatively treating the interaction of an atomic electron with the quantized radiation field, which may contain high-intensity components [3]. In the course of eliminating the minimal coupling terms of the quantized field, the interaction with the radiation is condensed to a space-translated “multiphoton effective potential”, which represent the vortices of multiphoton interaction (for an illustration see Figure 1). In our formalism the system “electron + (strong) laser mode(s) + mode(s) of the scattered radiation” has a natural basis set of entangled Coulomb-Volkov type states, whose photon part is in a multimode squeezed coherent state. According to this result, our model may also serve as a proper “microscopic background” of various strong-field phenomena, like above-threshold ionization (ATI) or high-harmonic generation (HHG). The derived strong-field Kramers-Heisenberg formula inherently desribes the optional appearance of the Cooper minimum in the HHG spectrum. The presented formalism may contibute to a more fundamental level of the theoretical description and understanding of photon-electron interactions in high-intensity radiation fields [3].

Figure 1. This 3D figure illustrates the temporal evolution of the expectation value of the multiphoton effective potential (laser-dressed Coulomb potential   with  ) in Heisenberg picture. We have taken  , and   for the inducing Ti:Sa laser parameters, in which case the amplitude of the free electron oscillation is 9 times larger than the Bohr radius, and assumed a Gaussian envelope  , which corresponds to 2.3 cyles full temporal width at half maximum. For a better visualization, we have chosen   for the cylindrical coordinate. This figure illustrates, that the effective potential vanishes before and after the external pulse, in contrast to the usual Kramers-Henneberger space translated potential.

Optical realization of a chaotic quantum protocol. — Iterated quantum protocols with measurement-based selection lead to deterministic chaos for the evolving pure state representing an ensemble of qubits. Deterministic chaos for the pure quantum state may lead to ergodic evolution in the sense that initial states from any small area on the Bloch sphere will cover the whole sphere after a finite number of iterations. We realized two steps of an ergodic protocol in a photonic experiment, where initial qubit states were encoded in the polarization and path degrees of freedom of down-converted photons stemming from a parametric process. We numerically analyzed the effect of noise on the time evolution and showed that the protocol, described by a Lattès map, remains quasi-ergodic for any initial state if the initial noise is small. The tomographic reconstruction of the quantum states throughout the evolution was consistent with simulations and thus the ergodicity of the quantum dynamics was demonstrated [4].

Optical realization of quantum walks on fractal graphs. — Photon propagation through an array of coupled waveguides arranged in various fractal patterns serves as a useful ‘optical simulator’ for revealing insights into quantum transport in complex scenarios. An independent research group tested recurrence for continuus-time quantum walks on Sierpiński gaskets and carpets in an optical experiment, corresponding to our earlier work. We have highlighted the importance of this developement [5]. The ability to experimentally implement quantum walks on complicated graphs may accelerate the design and testing of artificial 2D materials and algorithms based on quantum walks.

Electron-phonon entanglement in 1D systems. — We investigated the entanglement between electrons and phonons in a one dimensional system. The electron subsystem has been described by the Luttinger theory. We investigated the entanglement entropy, the negativity and the mutual information. The entanglement negativity increases with the electron-phonon coupling strength   and diverges with the Wentzel-Bardeen singularity. The mutual information decrease with the temperature and reaches a constant nonzero value in the high temperature limit, wich is the consequence of the infinite linear electron spectrum of the Luttinger model. The negativity decrease with the temperature, and becomes exactly zero above a temperature limit. The temperature limit depends on the system size. If the electron-electron interaction is screened enough the limit temperature remains finite. This means, in certain coupled electron phonon systems the electrons and the phonons become non-entangled over a limit temperature [6].

Quantum entanglement and its use it quantum metrology. — We worked on detecting entanglement in cold gases [7]. Our conditions have been tested in systems that create Dicke states. The condition detects bipartite entanglement between two spatially separated part of the ensemble. We also present  criteria that detect Einstein-Podolsky-Rosen (EPR) steering in such systems. Our criteria are resistant to the usual imperfections of the experiments, such as the nonzero variance of the particle number and the fact that not the entire state lives in the spatial mode in the Bose-Einstein condensate.
We also worked on the relation of entanglement and metrology via the formalism using the quantum Fisher information [8]. We presented a family of weakly entangle quantum states, called bound entangled states, that are more useful for metrology than separable states. In the limit of large dimensions, they are maximally useful. The family of states is known analytically, thus we can carry our calculations for large systems. Before, presented in a previous publication, we found similar states numerically, but could consider only relatively small systems.

We also worked on uncertainty relations with the quantum Fisher information, using the knowledge that the quantum Fisher information is the convex roof of the variance times four [9]. Starting from the Robertson-Schrödinger relation, we present  further uncertainties with the convex roof of the bound. We gain new insights on the Cramér-Rao bound. We strengthen the Robertson-Schrödinger uncertainty with a concave roof of the bound. We also present a novel uncertainty that is the sum of two variances and a quantum Fisher information term bounded by a constant. Finally, we show that the violation of some entanglement criteria implies that the quantum state is more useful than certain relevant subsets of separable states.

References.

[1] DOI: 10.1103/PhysRevB.104.054209

[2] https://arxiv.org/abs/2110.01985

[3] https://doi.org/10.3390/photonics8070269

Varró S, Quantum optical aspects of high-harmonic generation. Photonics 2021, 8 (7), 269.

[4] DOI: 10.1088/1367-2630/ac15b4

[5] https://doi.org/10.1038/s41566-021-00868-x
Tamás Kiss and Igor Jex, Photons walk on fractal graphs, Nature Photonics 15, 638 (2021)

[6] Gergő Roósz and Carsten Timm Phys. Rev. B 104, 035405 (2021)

[7] G. Vitagliano, M. Fadel, I. Apellaniz, M. Kleinmann, B. Lücke, C. Klempt, G. Tóth, Detecting Einstein-Podolsky-Rosen steering and bipartite entanglement in split Dicke states, arXiv:2104.05663.

[8] K. F. Pál, G. Tóth, E. Bene, T. Vértesi, Bound entangled singlet-like states for quantum metrology, Phys. Rev. Res. 3, 023101 (2021); arXiv:2002.12409. DOI: 10.1103/PhysRevResearch.3.023101

[9] G. Tóth and F. Fröwis, Uncertainty relations with the variance and the quantum Fisher information based on convex decompositions of density matrices, Phys. Rev. Res., in press; arXiv:2109.06893.

2020

Topological delocalization in the completely disordered two-dimensional quantum walk. — In low dimensional quantum systems, spatial disorder generically leads to Anderson localization, inhibiting spatial spread of wavefunctions.  This also occurs in two-dimensional quantum walks, versatile toy models for periodically driven quantum systems. We have found [1] that increasing spatial disorder to the maximum possible value (Haar random coin operators), leads to a delocalization: a diffusive spread of an initially localized wavepacket instead of Anderson localizaiton. This delocalization happens because maximal disorder places the quantum walk to a critical point between different anomalous Floquet-Anderson insulating topological phases. We have previously observed topological delocalization in a simpler quantum walk, using  time-evolution  of  the  wavefunctions  and  level  spacing  statistics. We have now calculated the topological invariants of disordered quantum walks using scattering theory, substantiating the topological interpretation of the delocalization, and finding its signatures in the finite-size scaling of transmission. We have shown criticality of the Haar random quantum walk by calculating the critical exponent η in three different ways and found η ≈ 0.52 as in the integer quantum Hall effect. Our results showcase how theoretical ideas and numerical tools from solid-state physics can help us understand spatially random quantum walks.

Figure 1. Position distribution of the Haar random quantum walk after 10000 timesteps

Ex ante versus ex post equilibria in classical Bayesian games with a nonlocal resource. — The relation of nonclassical correlations such those of Einstein-Podolsky-Rosen type to the classical theory of Bayesian games is getting an increasing research attention. As a contribution to this line of research we have analyzed the difference between the so-called ex ante and ex post equilibria in classical Bayesian games played with the assistance of a nonlocal (quantum or no-signaling) resource. In physics, the playing of these games is known as performing bipartite Bell-type experiments. By analyzing the Clauser-Horn-Shimony-Holt game, we have found a constructive procedure to find two-person Bayesian games with a nonlocal (ie, no-signaling, and, in many cases, quantum) advantage. Most games of this kind known from the literature can be constructed along this principle. Our construction can be applied to find further scenarios and protocols in which quantum correlations can be useful if realized. In addition we have found that the already known scenarios share the  property that their relevant ex ante equilibria are ex post equilibria as well. We have found, however, a different type of game, based on the Bell theorem by Vértesi and Bene, which does not have the latter property: The ex ante and ex post equilibria differ. [2]

Complete classification of trapping coins for quantum walks on the two-dimensional square lattice. — One of the unique features of discrete-time quantum walks is called trapping, meaning the inability of the quantum walker to completely escape from its initial position, although the system is translationally invariant. The effect is dependent on the dimension and the explicit form of the local coin. A four-state discrete-time quantum walk on a square lattice is defined by its unitary coin operator, acting on the four-dimensional coin Hilbert space. The well-known example of the Grover coin leads to a partial trapping, i.e., there exists some escaping initial state for which the probability of staying at the initial position vanishes. On the other hand, some other coins are known to exhibit strong trapping, where such an escaping state does not exist. We present a systematic study of coins leading to trapping, explicitly construct all such coins for discrete-time quantum walks on the two-dimensional square lattice, and classify them according to the structure of the operator and the manifestation of the trapping effect. We distinguish three types of trapping coins exhibiting distinct dynamical properties, as exemplified by the existence or nonexistence of the escaping state and the area covered by the spreading wave packet. [3]

Optimization of multiplexed single-photon sources operated with photon-number-resolving detectors. — Detectors inherently capable of resolving photon numbers have undergone a significant development recently, and this is expected to affect multiplexed periodic single-photon sources where such detectors can find their applications. We analyze various spatially and time-multiplexed periodic single-photon source arrangements with photon-number-resolving detectors, partly to identify the cases when they outperform those with threshold detectors. We develop a full statistical description of these arrangements in order to optimize such systems with respect to maximal single-photon probability, taking into account all relevant loss mechanisms. The model is suitable for the description of all spatial and time multiplexing schemes. Our detailed analysis of symmetric spatial multiplexing identifies a particular range of loss parameters in which the use of the new type of detectors leads to an improvement. Photon number resolution opens an additional possibility for optimizing the system in that the heralding strategy can be defined in terms of actual detected photon numbers. Our results show that this kind of optimization opens an additional parameter range of improved efficiency. Moreover, this higher efficiency can be achieved by using less multiplexed units, i.e., smaller system size as compared to threshold-detector schemes. We also extend our investigation to certain time-multiplexed schemes of actual experimental relevance. We find that the highest single-photon probability is 0.907 that can be achieved by binary bulk time multiplexers using photon-number-resolving detectors. [4]

2019

Mesurement-induced nonlinear transformations. — By involving two or more identical copies of qubits in the same state, it is possible to induce nonlinear quantum state transformations by applying an entangling unitary operation pairwise, combined with a postselection scheme conditioned on the measurement result obtained on one of the qubits of the pair. Such maps play a central role in distillation protocols used for quantum key distribution. We determined that such protocols may exhibit sensitive, quasi-chaotic evolution not only for pure initial states but also for mixed states, i.e., the complex dynamical behavior is not destroyed by small initial uncertainty. We showed that the appearance of sensitive, complex dynamics associated with a fractal structure in the parameter space of the system has the character of a phase transition. The purity of the initial state plays the role of the control parameter, and the dimension of the fractal structure is independent of the purity value after passing the phase transition point (Fig.1). The critical purity coincides with the purity of a repelling fixed point of the dynamics, and we show that all the pre-images of states from the close neighborhood of pure chaotic initial states have purity larger than this. Initial states from this set can be considered as quasi-chaotic .

Figure 1. The fractal dimension D_bc of the border between the different convergence regions as a function of the initial purity. The error bars indicate the range of numerically calculated values D_bc. The black squares correspond to the mean value of the 37 data points for each initial purity. For initial purities above 0.78, D_bc is fluctuating around the average value 1.561 (solid line). For P < 0.76, where the structure is no longer a fractal, D_bc equals 1 within the statistical error of the numerical method.

We experimentally realized a nonlinear quantum protocol for single-photon qubits with linear optical elements and appropriate measurements. Quantum nonlinearity was induced by postselecting the polarization qubit based on a measurement result obtained for the spatial degree of freedom of the single photon which played the role of a second qubit. Initially, both qubits were prepared in the same quantum state and an appropriate two-qubit unitary transformation entangled them before the measurement of the spatial part. We analyzed the result by quantum state tomography of the polarization degree of freedom. We then demonstrated the usefulness of the protocol for quantum state discrimination by iteratively applying it to either of two slightly different quantum states which rapidly converged to different orthogonal states by the iterative dynamics .

Nonlinear optical processes. — We implemented the pseudospectral method for the Finite Difference Frequency Domain method (FDFD) and hence the resulting method is called Pseudospectral Frequency Domain method (PSFD). We compared the PSFD method with the FDFD method in terms of the numerical phase velocity and anisotropy. The main advantage of our method compared to finite differences is the significantly larger accuracy at the same grid resolution. We extended our method for the nonlinear process (NL-PSFD) of Second Harmonic Generation (SHG). We showed how a plane wave source at oblique incidence can be implemented and we discussed its performance for tilted Quasi-Phase Matched (QPM) grating. Finally, we proposed a specific method deduced from NL-PSFD for large volume simulation where only second order nonlinearity is structured spatially, and simulated a two-dimensional nonlinear photonic crystal (Fig.2) .

Figure 2. SHG process in a 2D nonlinear photonic crystal. The domain inversion is carried out on a centered rectangular lattice, in a circular pattern. The left part of the figure shows the incoming fundamental wave, the middle represents the nonlinear photonic crystal, while the right part shows the generated second harmonic wave.

Topological quantum gates. — Topological properties of quantum systems could provide protection of information against environmental noise, and thereby drastically advance their potential in quantum information processing. Most proposals for topologically protected quantum gates are based on many-body systems, e.g., fractional quantum Hall states, exotic superconductors, or ensembles of interacting spins, bearing an inherent conceptual complexity. We proposed and studied a topologically protected quantum gate, based on a one-dimensional single-particle tight-binding model, known as the Su-Schrieffer-Heeger chain. The proposed Y gate acts in the two-dimensional zero-energy subspace of a Y junction assembled from three chains, and is based on the spatial exchange of the defects supporting the zero-energy modes. With numerical simulations, we demonstrated that the gate is robust against hopping disorder but is corrupted by disorder in the on-site energy. Then we show that this robustness is topological protection, and that it arises as a joint consequence of chiral symmetry, time-reversal symmetry, and the spatial separation of the zero-energy modes bound to the defects. This setup will most likely not lead to a practical quantum computer; nevertheless it does provide valuable insight to aspects of topological quantum computing as an elementary minimal model. Since this model is noninteracting and nonsuperconducting, its dynamics can be studied experimentally, e.g., using coupled optical waveguides .

2018

Measurement-induced nonlinear transformations — We considered the task of deciding whether an unknown qubit state falls in a prescribed neighborhood of a reference state. If several copies of the unknown state are given and we can apply a unitary operation pairwise on them combined with a postselection scheme conditioned on the measurement result obtained on one of the qubits of the pair, the resulting transformation is a deterministic, nonlinear, chaotic map in the Hilbert space. We derived a class of these transformations capable of orthogonalizing nonorthogonal qubit states after a few iterations. These nonlinear maps orthogonalize states which correspond to the two different convergence regions of the nonlinear map. Based on the analysis of the border (the so-called Julia set) between the two regions of convergence, we showed that it is always possible to find a map capable of deciding whether an unknown state is within a neighborhood of fixed radius around a desired quantum state. We analyzed which one- and two-qubit operations would physically realize the scheme. It is possible to find a single two-qubit unitary gate for each map or, alternatively, a universal special two-qubit gate together with single-qubit gates in order to carry out the task. We note that it is enough to have a single physical realization of the required gates due to the iterative nature of the scheme.



Figure 1. The decomposition of the relevant map f into the subsequent actions of a contracting two-qubit operation and a single-qubit unitary operation. (a) The effect of the decomposition on the complex plane (projection of the Bloch sphere), representing the initial states of the qubit. States within the solid circle are matched. (b) The same decomposition represented on the Bloch sphere.

Quantum walks — Measurements on a quantum particle unavoidably affect its state, since the otherwise unitary evolution of the system is interrupted by a nonunitary projection operation. To probe measurement-induced effects in the state dynamics using a quantum simulator, the challenge is to implement controlled measurements on a small subspace of the system and continue the evolution from the complementary subspace. A powerful platform for versatile quantum evolution is represented by photonic quantum walks because of their high control over all relevant parameters. However, measurement-induced dynamics in such a platform have not yet been realized. We participated in the implementation (at the University of Paderborn) of controlled measurements in a discrete-time quantum walk based on time-multiplexing. This was achieved by adding a deterministic outcoupling of the optical signal to include measurements constrained to specific positions resulting in the projection of the walker’s state on the remaining ones. With this platform and coherent input light, we experimentally simulated measurement-induced single-particle quantum dynamics. We demonstrated the difference between dynamics with only a single measurement at the final step and those including measurements during the evolution. To this aim, we studied recurrence as a figure of merit, that is, the return probability to the walker’s starting position, which was measured in the two cases. We tracked the development of the return probability over 36 time steps and observed the onset of both recurrent and transient evolution as an effect of the different measurement schemes, a signature which only emerges for quantum systems. Our simulation of the observed one-particle conditional quantum dynamics does not require a genuine quantum particle but was demonstrated with coherent light.



Figure 2. Schematic of the experimental setup of the time-multiplexed quantum walk with active in- and outcoupling realized by two EOMs (electro-optical modulators). The active control of the switches allows to implement in the time domain both the continual and reset measurement schemes. HWP, half-wave plate; PBS, polarizing beam splitter; SMF, single-mode fiber; SNSPDs, superconducting nanowire single-photon detectors. 

Ro-vibrational quantum states in molecules — We determined the internal-axis system (IAS) of molecules with a large amplitude internal motion (LAM) by integrating the kinematic equation of the IAS by Lie-group and Lie-algebraic methods. Numerical examples on hydrogen peroxide, nitrous acid, and acetaldehyde demonstrate the methods. By exploiting the special product structure of the solution matrix, we devised simple methods for calculating the transformation to the rho-axis system (RAS) along with the value of the parameter ρ characterizing a RAS rotational-LAM kinetic energy operator. The parameter ρ so calculated agrees exactly with that one obtained by the Floquet method as shown in the example of acetaldehyde. We gave geometrical interpretation of ρ. We numerically demonstated the advantageous property of the RAS over the IAS in retaining simple periodic boundary conditions.

Nanophotonics — Nonlinear second harmonic wave generation (SHG) has been thoroughly examined in one dimension both analytically and numerically. Recently, the application of advanced domain poling techniques enabled the fabrication of two-dimensional (2D) patterns of the sign of the nonlinear coefficient in certain nonlinear crystals, such as LiNbO3 and LiTaO3 . This method can be used to achieve quasi phase matching in SHG and hence amplification of the second harmonic fields in 2D. We have worked out a true vectorial numerical method for the simulation of SHG by extending the finite difference frequency domain method (FDFD). Our nonlinear method (NL-FDFD) operates directly on the electromagnetic fields, uses two meshes for the simulation (for ω and 2ω fields), and handles the nonlinear coupling as an interaction between the two meshes. Final field distributions can be obtained by a small number of iteration steps. NL-FDFD can be applied in arbitrarily structured linear media with an arbitrarily structured χ^(2) component both in the small conversion efficiency and the pump depleted cases.



Figure 3. Magnitude of the Ez field components for  (a) fundamental wave (b) second harmonic wave at the  resonant frequency for five arrays of cylinders. We show here the result of a model calculation: the underlying dielectric structure consists of periodic arrays of nonlinear cylinders, it is infinite in the x-direction and there are five periods in the y-direction. The fundamental wave propagates in the positive y-direction, and it can be tilted from normal incidence. At certain angles and frequencies the structure exhibits double resonance: the reflectivity is close to unity both for the fundamental and for the second harmonic wave
 

2017

Measurement-induced non-linear transformations. — We proposed a cavity quantum electrodynamical scenario for implementing a Schrödinger microscope capable of amplifying differences between non-orthogonal atomic quantum states. The scheme involves an ensemble of identically prepared two-level atoms interacting pairwise with a single mode of the radiation field as described by the Tavis-Cummings model (Fig. 1).

Figure 1. Illustration of the scheme. Two two-level atoms in the same state interact with the cavity field prepared in a coherent state. Before the interaction, a unitary gate is applied to one of the atoms, and after the interaction and the projection of the field onto the initial coherent state, this same atom is projected onto its ground state. Finally, the other atom is left in a non-linearly transformed state.

We showed that by repeated measurements of the cavity field and of one atom within each pair, a measurement-induced non-linear quantum transformation of the relevant atomic states can be realized. The intricate dynamical properties of this non-linear quantum transformation, which exhibits measurement-induced chaos, allow approximate orthogonalization of atomic states by purification after a few iterations of the protocol and, thus, the application of the scheme for quantum state discrimination.

Topological phases. — We discovered topological features of the Hofstadter butterfly spectra of periodically driven systems. The butterfly is the fractal spectrum of energy eigenstates of a quantum lattice system in a magnetic field. It was discovered numerically (1976, predating the word "fractal"), analyzed analytically (contributing to the topological understanding of the quantum Hall effect), and it is about to be observed experimentally on laser-trapped cold atoms and in graphene. We found that in periodically driven systems, where the drive is very far from just a perturbation, the Hofstadter butterfly can "take flight", i.e., can "wind" in quasienergy (Fig. 2). This behaviour is closely related to a recently discovered topological invariant unique to such non-perturbatively driven systems, and gives us a way to numerically evaluate and perhaps experimentally observe this invariant in an efficient way.

Figure 2. The spectrum of quasienergies of a periodically driven system (quantum walk) can wind as a function of applied magnetic field. The winding is quantized, and reveals a bulk topological invariant of the system.

Ro-vibrational quantum states in molecules. — Recently, a general expression for Eckart-frame Hamilton operators has been obtained by the gateway Hamiltonian method. The kinetic energy operator in this general Hamiltonian is nearly identical to that of the Eckart-Watson operator even when curvilinear vibrational coordinates are employed. Its different realizations correspond to different methods of calculating Eckart displacements. There are at least two different methods for calculating such displacements: rotation and projection. In our work, the application of Eckart Hamiltonian operators constructed by rotation and projection was numerically demonstrated in calculating vibrational energy levels. The numerical examples confirm that there is no need for rotation to construct an Eckart ro-vibrational Hamiltonian. The application of the gateway method is advantageous even when rotation is used since it obviates the need for differentiation of the matrix rotating into the Eckart frame. Simple geometrical arguments explain that there are infinitely many different methods for calculating Eckart displacements. The geometrical picture also suggests that a unique Eckart displacement vector may be defined as the shortest (mass-weighted) Eckart displacement vector among Eckart displacement vectors corresponding to configurations related by rotation. Its length, as shown analytically and demonstrated by numerical examples, is equal to or less than that of the Eckart displacement vector one can obtain by rotation to the Eckart frame.

Nanophotonics. — We have worked out a true vectorial numerical method for the simulation of the non-linear second harmonic generation process by extending the finite difference frequency domain method (FDFD). Our non-linear method (NL-FDFD) operates directly on the electromagnetic fields, uses two meshes for the simulation (for ω and 2ω fields) and handles the non-linear coupling as an interaction between the two meshes. Final field distributions can be obtained by a small number of iteration steps. NL-FDFD can be applied in arbitrarily structured linear media with an arbitrarily structured χ (2) component both in the small-conversion-efficiency and the pump-depleted cases.