2023
Quantum annealing with heterogeneous fields. — In transverse-field Ising models, disorder in the couplings gives rise to an unfavorable, slower-than-algebraic scaling of the density of defects produced when the system is driven through its quantum critical point. By applying Kibble-Zurek theory and numerical calculations, we demonstrated in the one-dimensional model that the scaling of defect density with annealing time can be made algebraic by balancing the coupling disorder with suitably chosen inhomogeneous driving fields. We also studied defect production during an environment-temperature quench of the open variant of the model in which the system is slowly cooled down to its quantum critical point. According to our results, uncorrelated disorder induces a logarithmic temporal decrease of the defect density, while balanced disorder leads again to an algebraic decay [1].
Renormalization theory of disordered contact processes. — Motivated by long-range dispersal in ecological systems, we formulated and applied a general strong-disorder renormalization group framework to describe one-dimensional disordered contact processes with heavy-tailed (such as power law, stretched exponential, and log-normal) dispersal kernels, widely used in ecology. The focus was on the close-to-critical scaling of the order parameters, including the commonly used density, as well as the less known persistence. Our results reveal that the more slowly decaying dispersal kernels lead to faster-vanishing densities as the critical point is approached. The persistence, however, shows an opposite tendency: the broadening of the dispersal makes its decline sharper at the critical point [2].
Correcting coherent and readout errors in the surface code. — Quantum Error Correction is a crucial component of large-scale quantum computation, the only way to achieve the low error rates required for precise algorithms. The surface code is the currently leading quantum error correction protocol, which has recently been implemented on various quantum computer prototypes. Although it is thoroughly understood how the surface code offers protection of quantum data against incoherent (random Pauli) errors, the level of protection it ensures against coherent errors is less well known. We tested numerically the performance of the surface code against a combination of coherent and readout errors, using a recently developed simulation approach (mapping the quantum state of the processor to a multifermion system). We found that there is an error correction threshold here, with a value close to that of the corresponding incoherent error channel [3].
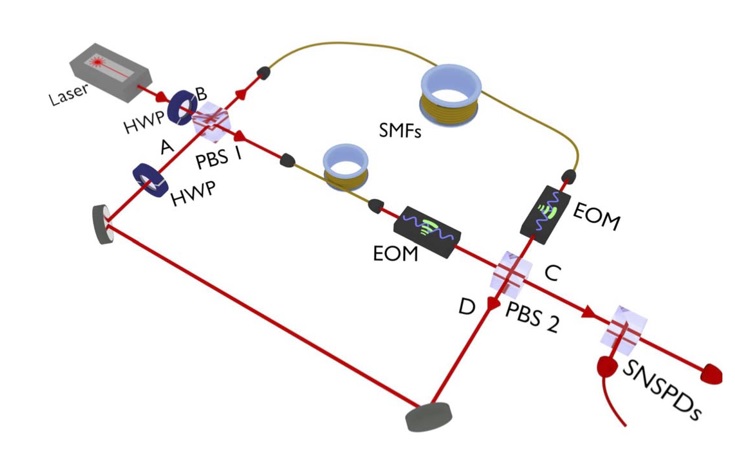
Sequential unsharp measurement of photon polarization. – We propose a general experimental scheme based on binary trees of partially polarizing beam splitters (PPBSs) for realizing sequential unsharp measurements of photon polarization. The sharpnesses and the bases of the particular photon polarization measurements can be chosen arbitrarily by using corresponding PPBSs and phase plates in the setup. In the limit of low sharpnesses the scheme can realize sequential weak measurements, too. We develop a general formalism for describing sequential unsharp measurements of photon polarization in which the particular unsharp measurements are characterized by appropriate measurement operators. We show that a straightforward experimental realization of this model is the proposed scheme. In this formalism the output polarization states after the sequential measurement and any correlation functions characterizing the measurement results can be easily calculated. Our model can be used for analyzing the consequences of applying postselection and reselection in the measurement. We derive the anomalous mean value for an unsharp polarization measurement with postselection and the anomalous second-order correlation function for the sequential unsharp measurement of photon polarization with reselection. We show that these anomalies can be easily measured using the proposed scheme. [4]
Multiplexed single-photon sources with optimal structure. – We consider novel types of spatially multiplexed single-photon sources based on output-extended incomplete binary-tree multiplexers containing general asymmetric routers where the construction of the multiplexers takes into account the total transmission efficiencies of the multiplexer arms at which a novel router can be added to the system. After selecting the multiplexer that outperforms the others, we identify the ranges of the loss parameters for which the application of the selected multiplexer leads to single-photon sources with higher single-photon probabilities and lower multiphoton noise than that can be achieved by using asymmetric multiplexers. We show that using the selected multiplexer is especially advantageous in the case of single-mode sources characterized by thermal statistics of the input photon pairs. We also reveal that the application of this multiplexer yields high performance single-photon sources even for suboptimal system sizes, which is a typical situation in current experiments. [5]
Entanglement in cold atoms. — We present a method to detect bipartite entanglement based on number-phase-like uncertainty relations in split spin ensembles. First, we derive an uncertainty relation that plays the role of a number-phase uncertainty for spin systems. It is important that the relation is given with well-defined and easily measurable quantities, and that it does not need assuming infinite dimensional systems. Based on this uncertainty relation, we show how to detect bipartite entanglement in an unpolarized Dicke state of many spin-1/2 particles. The particles are split into two subensembles, then collective angular momentum measurements are carried out locally on the two parts. First, we present a bipartite Einstein-Podolsky-Rosen (EPR) steering criterion. Then, we present an entanglement condition that can detect bipartite entanglement in such systems. We demonstrate the utility of the criteria by applying them to a recent experiment given in K. Lange et al. [Science 360, 416 (2018)] realizing a Dicke state in a Bose-Einstein condensate of cold atoms, in which the two subensembles were spatially separated from each other. Our methods also work well if split spin-squeezed states are considered. We show in a comprehensive way how to handle experimental imperfections, such as the nonzero particle number variance including the partition noise, and the fact that, while ideally BECs occupy a single spatial mode, in practice the population of other spatial modes cannot be fully suppressed. [6]
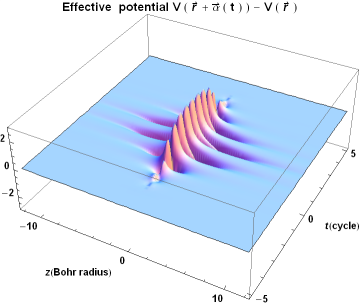
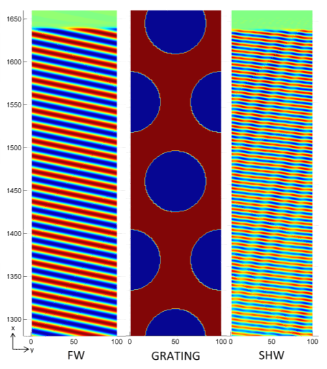
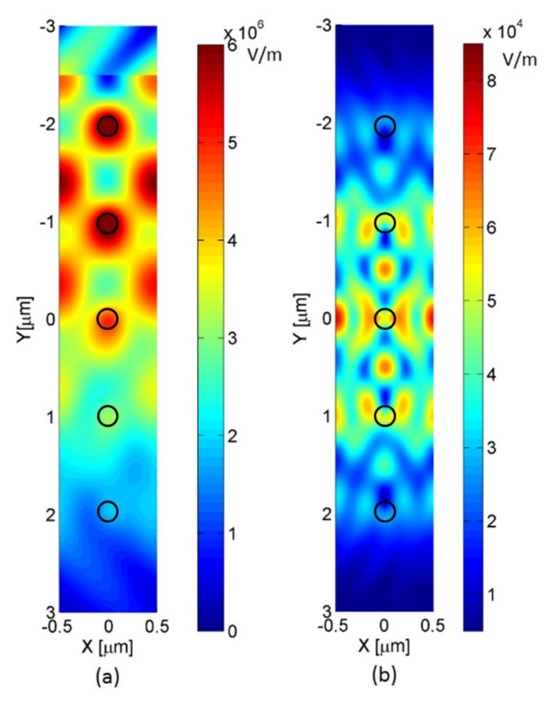
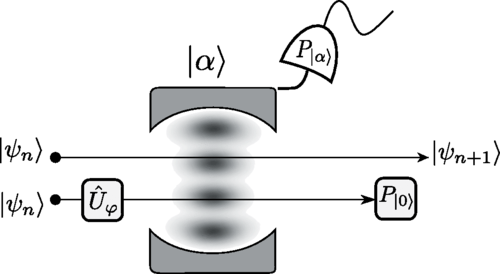
Propagating single photons from an open cavity. — We have derived and analyzed models for the system of an atom trapped in a cavity, featuring a semitransparent mirror and driven by laser pulses allowing the production of a single photon leaking out from the cavity. We introduced true-mode, inside-outside, and pseudomode representations for describing the system from first principles. From the exact modes of the system (the true-mode representation), we explicitly introduce the cavity-reservoir coupling, which allows one to describe the dynamics without any a priori approximations. We have demonstrated that under suitable approximations that we formulate, these different representations give accurate results that are similar to each other, yet generally differ. We particularly analyze a high-Q cavity scenario and show that this requirement alone, in general, is not enough for these approximate models to work. This is especially significant for the models where we consider cavities with higher losses and mode overlaps, namely, cavities with low refractive indices, such as plasmonic cavities. In nanophotonics, it is common to transpose these approximate models derived for optical cavities to plasmonic cavities. However, as shown here, these approximate models already yield different predictions for optical cavities with relatively high transmission. In the literature, it is common to phenomenologically introduce the pseudomode representation. However, this kind of phenomenological approach does not provide the full description of the produced photon, namely, the outgoing photon shape in the frequency domain. In contrast, here, we recover the phenomenological model derived from first principles; moreover, it is complemented with the complete description of the system, including the full characteristics of the photon in the time domain as well as in the frequency domain. This derivation justifies explicitly the Markov approximation producing an input-output relation from first principles via the nontrivial cavity-reservoir coupling. This allows a precise definition of the propagating outside photon state. Finally, concepts, such as the Poynting vector, photon flux, input-output operators, and photon state, that characterize the propagation of the resulting leaking photons have been defined and connected: We have formulated an input-output relation taking into account the propagating effects, which allows a direct interpretation of the out operator through the Poynting vector and the photon flux. The generated flux is then determined from the quantum average of the dynamics of the photon number in the cavity, which results from a standard master equation [7].
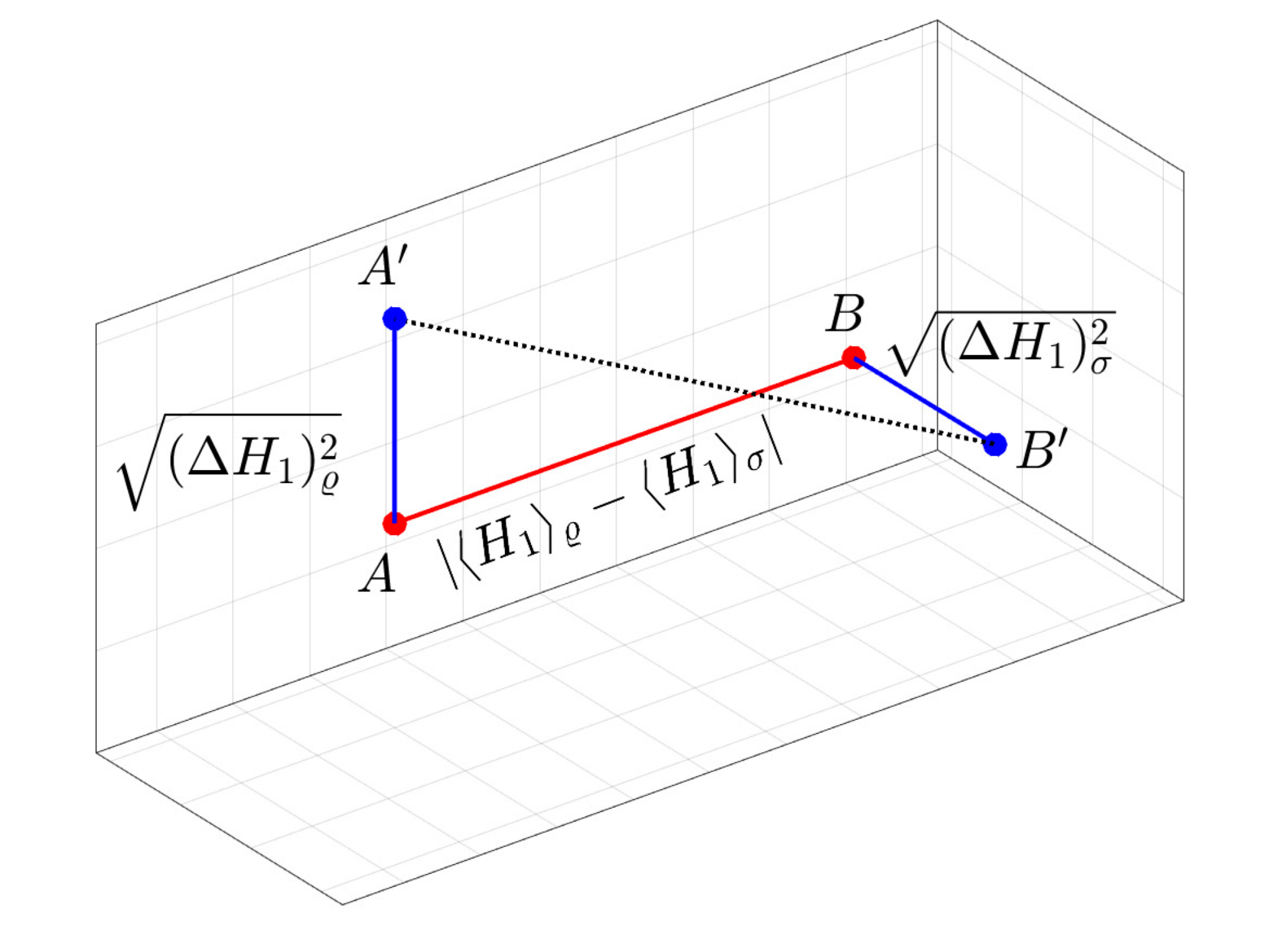
Quantum Optimal Transport. — In probability and statistics, defining the distance of probability measures or probability density functions plays a central role. However, many traditional distance definitions do not effectively characterize the difference between two density functions. For example, if two probability density functions p (x) and q(x) have disjoint support, that is, p(x)=0 whenever q(x)>0, at the usual distances p(x) and q(x) distance is maximal, regardless of how far the supports of p and q are from each other. Let e.g., p(x) is a function that is non-zero only for 0<x<1, while q(x) is non-zero only for 10<x<11. The distance will be maximal in the same way as if q(x) were non-zero only for 100<x<101. This phenomenon is usually expressed as the distance between p and q being insensitive to the underlying metric. The problem is remedied by the so-called Wasserstein distance defined in optimal transport theory, the basic idea of which can be illustrated with the following example. Suppose we have a pile of sand of a unit volume described by the density function p(x). We want to move this pile of sand to another place, and we expect it to have a density q(x). The transport is characterized by a cost function, which of course depends on the distance between the two piles of sand, i.e., the underlying metric. The Wasserstein distance is essentially the total cost of moving the sand from a pile with a distribution p(x) to another one with a distribution q(x). The Wasserstein distance can be defined in several ways for the quantum case. One of these possibilities is when the expected value of an operator is minimized on bipartite quantum states with a given marginal. A surprising feature of the so-called quantum Wasserstein-2 distance is that the self-distance, i.e., the distance of a quantum state from itself, can be non-zero. For the quantity defined by De Palma and Trevisan, the square of the self-distance is equal to the Wigner-Yanase skew information. In [8] Géza Tóth and József Pitrik showed that if we limit the optimization to the set of separable states, we get a new and interesting quantity. The paper examined the properties of the quantity and its relation to entanglement theory. They proved that the square of the self-distance is equal to the quantum Fisher information, a central notion in quantum metrology, over four, if we consider a single local operator to define the cost operator.
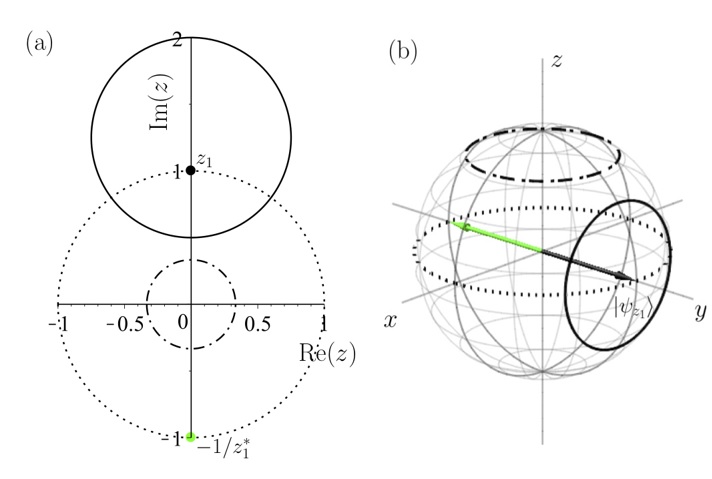
In the paper [9] the Wasserstein isometries of the quantum bit state space is described with respect to distinguished cost operators. A Wigner-type result is derived for the cost operator involving all the Pauli matrices: in this case, the isometry group consists of unitary or anti-unitary conjugations. In the Bloch sphere model this means that the isometry group coincides with the classical symmetry group O(3). On the other hand, for the cost generated by the qubit “clock” and “shift” operators, they discovered non-surjective and non-injective isometries as well, beyond the regular ones. This phenomenon mirrors certain surprising properties of the quantum Wasserstein distance.
References:
[1] R. Juhász, G. Roósz, Reducing defect production in random transverse-field Ising chains by inhomogeneous driving fields, Phys. Rev. B 108, 224203 (2023). https://doi.org/10.1103/PhysRevB.108.224203
[2] R. Juhász, Renormalization theory of disordered contact processes with heavy-tailed dispersal, Phys. Rev. Research 5, 033157 (2023). https://doi.org/10.1103/PhysRevResearch.5.033157
[3] Á. Márton, J.K. Asbóth, Coherent errors and readout errors in the surface code, Quantum 7, 1116 (2023). https://doi.org/10.22331/q-2023-09-21-1116
[4] P. Adam, L. Diósi, Sequential unsharp measurement of photon polarization, Phys. Rev. A 107, 063706 (2023). https://doi.org/10.1103/PhysRevA.107.063706
[5] P. Adam, M. Mechler, Single-photon sources based on incomplete binary-tree multiplexers with optimal structure, Optics Express 31, 30194 (2023). https://doi.org/10.1364/OE.496206
[6] G. Vitagliano, M. Fadel, I. Apellaniz, M. Kleinmann, B. Lücke, C. Klempt, G. Tóth, Number-phase uncertainty relations and bipartite entanglement detection in spin ensembles, Quantum 7, 914 (2023). https://doi.org/10.22331/q-2023-02-09-914
[7] A. Saharyan, B. Rousseaux, Z. Kis, S. Stryzhenko, and S. Guérin, Propagating single photons from an open cavity: Description from universal quantization, Phys. Rev. Research 5, 33056 (2023). https://doi.org/10.1103/PhysRevResearch.5.033056
[8] G. Tóth, J. Pitrik, Quantum Wasserstein distance based on an optimization over separable states, Quantum 7, 1143 (2023). https://doi.org/10.22331/q-2023-10-16-1143
[9] G.P. Gehér, J. Pitrik, T. Titkos, D. Virosztek, Quantum Wasserstein isometries on the qubit state space, J. Math. Anal. Appl. 522, 126955 (2023). https://doi.org/10.1016/j.jmaa.2022.126955