2018
Experiment on Cavity Quantum Electrodynamics with cold Rb atoms ― We set up a new laboratory for cavity QED experiments with ultracold Rb atoms. We realized the UHV system which is operated in the pressure range below 1e-10 mbar, and includes the magneto-optical trap and the in-vacuo high-finesse single-mode optical resonator. We completed the optical system which is based on three laser sources that are referenced to Rb resonance line by Doppler-free non-linear spectroscopy. By means of acousto-optical modulators we provide the narrow linewidth phase-locked laser sources at five different frequencies for atomic manipulation.

Fig. 1. Photo of the actual status of the cavity QED laboratory.
Cavity Quantum Electrodynamics, quantum critical phenomena. ― The quantum measurement back action noise effects on the dynamics of an atomic Bose lattice gas inside an optical resonator has been described by means of a hybrid model consisting of a Bose–Hubbard Hamiltonian for the atoms and a Heisenberg–Langevin equation for the lossy cavity field mode. Considering atoms initially being prepared in the ground state of the lattice Hamiltonian, we calculated the transient dynamics due to the interaction with the cavity mode. We showed that the cavity field fluctuations originating from the dissipative outcoupling of photons from the resonator lead to vastly different effects in the different possible ground state phases, i.e., the superfluid, the supersolid, the Mott- and the charge-density-wave phases. In the former two phases with the presence of a superfluid wavefunction, the quantum measurement noise appears as a driving term leading to depletion of the ground state. The time scale for the system to leave the ground state was presented in a simple analytical form. For the latter two incompressible phases, the quantum noise results in the fluctuation of the chemical potential. We derived an analytical expression for the corresponding broadening of the quasiparticle resonances. [Phys. Rev. A 97, 063602 (2018) ]
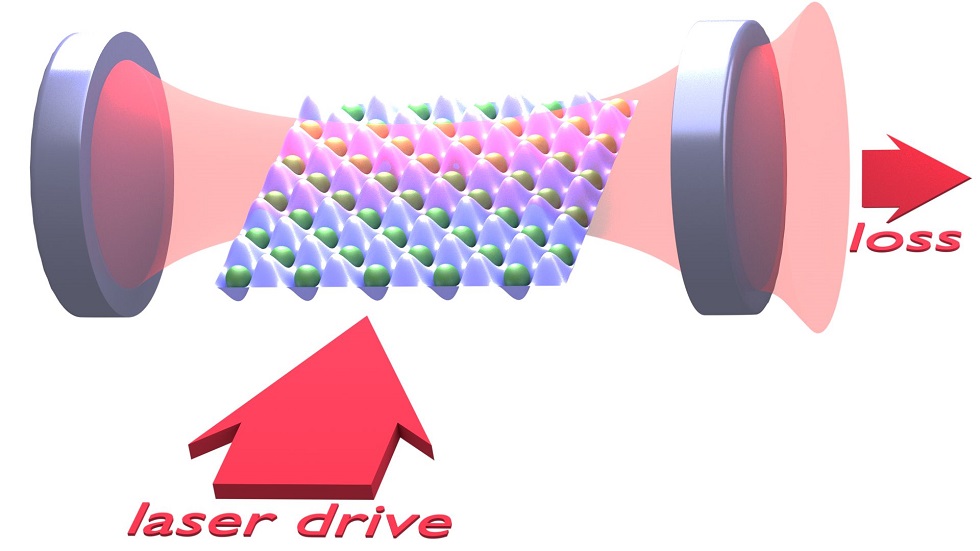
Fig. 2. Illustration of the coupled cavity Bose-Hubbard model setup. An atomic cloud is loaded into a square optical lattice, which is inside a single-mode high-Q Fabry-Pérot resonator. The period of the cavity mode is approximately equal to that of the optical lattice. The cavity is pumped from the side by light scattering off the atoms. The system is open, together with the external drive, the photons leak out from the cavity, resulting in heating and decoherence, or, in other terms, quantum measurement back action since the out coupled photons can be measured by classical detectors.
Ultracold gases, Bose-Einstein condensates. ― We studied quasiparticle scattering effects on the dynamics of a homogeneous Bose-Einstein condensate of ultracold atoms coupled to a single mode of an optical cavity. The relevant excitations, which are polariton-like mixed excitations of photonic and atomic density-wave modes, have been identified. All the first-order correlation functions were presented by means of the Keldysh Green’s function technique. Beyond confirming the existence of the resonant enhancement of Beliaev damping, we found a very structured spectrum of fluctuations. There is a spectral hole burning at half of the recoil frequency reflecting the singularity of the Beliaev scattering process. The effects of the photon-loss dissipation channel and that of the Beliaev damping due to atom-atom collisions could have been well separated. We showed that the Beliaev process does not influence the properties of the self-organization criticality. [Phys. Rev. A 98, 063608 (2018)]
(a)
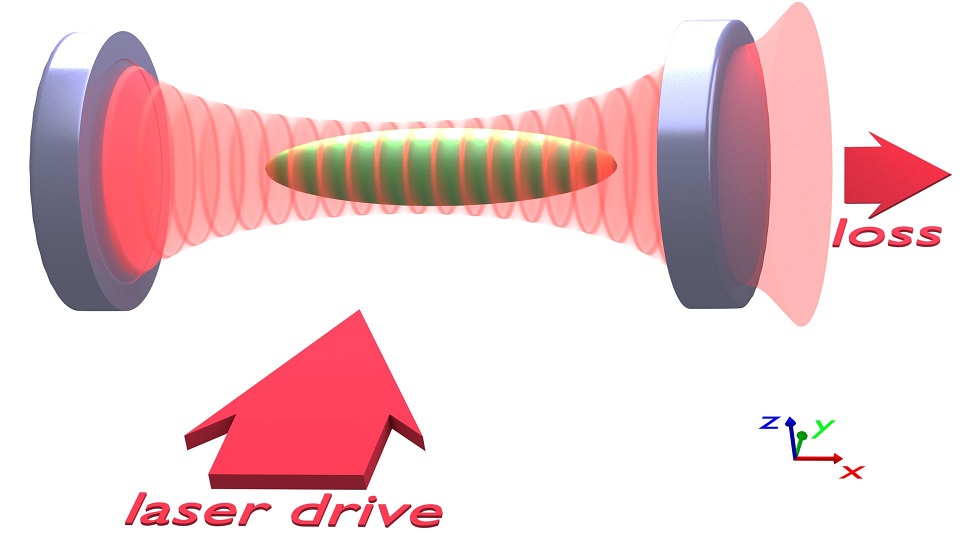
(b)
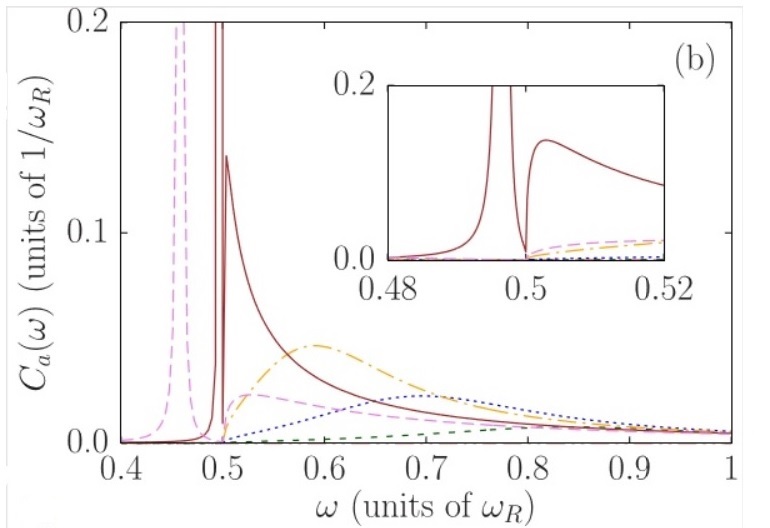
FIG. 3 (a) The schematic picture of an atomic ensemble inside a Fabry-Pérot cavity is pumped from the side by a laser close to resonance with the cavity. The atomic gas undergoes self-organization for strong enough laser drive: the atoms scatter photons from the laser to the cavity and may create a classical field serving as an optical lattice trapping them even further in the optimal scattering positions. (b) Spectrum of the quasiparticle excitation. Large detuning ∆C = 100 implies little mixing of the condensate quasiparticle with the photon mode. The enhanced Beliaev scattering process is manifested by the large peak, which exhibits a hole burning at 0.5. (All angular frequencies are expressed in units of the recoil frequency.) The correlation function is plotted for different coupling strengths y approaching the critical value yc: y = 0 (solid red), y/yc = 0.5 (short-dashed green), 0.7 (dotted blue), 0.8 (dashed-dotted orange), 0.9 (dashed-double-dotted brown), 0.95 (long-dashed magenta).
We studied the spin-1 bilinear–biquadratic model on the complete graph of N sites, i.e. when each spin is interacting with every other spin with the same strength. Because of its complete permutation invariance, this Hamiltonian can be rewritten as the linear combination of the quadratic Casimir operators of SU(3) and SU(2). Using group representation theory, we explicitly diagonalized the Hamiltonian and mapped out the ground-state phase diagram of the model. Furthermore, the complete energy spectrum, with degeneracies, was obtained analytically for any number of sites. [J. Phys. A: Math. Theor. 51, 105201 (2018) ]



