Holographic Quantum Field Theory Research Group

Group leader: Zoltán BAJNOK
The website of the group: https://wigner.hu/~bajnok/Hologroup/
Publications of the group: link to the database of the Hungarian Scientific Bibliography
According to the holographic conjuncture, our universe of three space dimensions and one time dimension might be equivalent to the four+one dimension universe, containing only gravity. We would be the holograms of four-dimensional objects in the gravitational universe - on its three-dimensional edge -and everything we do could be explained through higher- dimension gravitational processes.
Our research group has set the examination of such theories as its target. The holographic conjuncture could first be verified on the simplest building-blocks of the world. To our current knowledge, these elemental particles are the fermions - the 6-quark, the 3-neutrino, the electron, the muon and the tau - which interact by exchanging bosons (photons, gluons or weak bosons). The strength of the interaction is defined by the admission and absorption strength of the bosons, which is very small for the photon and great for the gluon, making exact calculations of relevant gluonic processes in the Large Hadron Collider impossible.
Our research group is examining a theory in which every fermionic particle has a bosonic partner and all emission strengths are equal. All studies so far have shown that this theory is the hologram of a higher-dimension gravitational theory. We have achieved quantum gravity by using a string theory and have, for now, found an exact description of the force between the two quarks that we are able to evaluate for weak interactions. Our "gravitational" calculations have been identical to the three-dimensional calculations of the hologram world, so we have confirmed both the holographic conjuncture and that our description is correct. In continuation, we would also like to examine our description in the strong interaction range. the difficulty of the problem is well characterised by the one-million-dollar prize that has been set for an exact description of the interaction between real quarks.
The electromagnetic, weak, strong and gravitational forces are the four fundamental interactions of Nature: The first two are unified by the electro-weak quantum gauge theory and have been tested with very high precision. The strong interaction is also formulated as a quantum gauge theory but tested analytically at high energies only, where the interaction is effectively weak. The gravitational interaction can be formulated as a classical gauge theory but does not allow a satisfactory quantum field-theoretical formulation. Thus the language of Nature seems to be gauge theories, but there is no analytically solved strongly interacting quantum gauge theory yet. The unification of all fundamental forces into one single theory is a dream of theoretical physicists. String theory, which replaces point particles with one-dimensional string-like objects could provide such a unification. Strings move in space-time such that they minimize the area of the two dimensional (2D) surface they sweep: the worldsheet. The theory can be formulated as a 2D quantum field theory on this worldsheet; however, consistent quantization requires the space-time to be 10 dimensional. In order to understand how 4D Minkowski space and the Standard Model emerge from this theory, one has to solve string theory on compactified curved backgrounds, which is one of the most relevant unsolved
problems in this field. It includes the determination of the masses of string excitations, such as gauge bosons and matter particles, and their interaction strengths. Ideally, it would explain the origin of the parameters of the Standard Model.
The holographic duality conjecture gives a hope to understand the strong interaction and quantum gravity in one turn, as it relates strongly-coupled gauge theories to semi-classical string theory, and the deeply quantum string theory to perturbative gauge theory. The duality is a kind of holography, as it proposes an equivalence between string theory in an open curved space and a strongly-coupled gauge theory living on the boundary of this space, in a way that is reminiscent of an optical hologram which stores a 3D imagine on a 2D holographic plate. The best established correspondence relates the maximally supersymmetric 4D quantum gauge theory to superstring theory on the product of the 5D anti de Sitter (AdS) space and the 5D sphere (AdS5×S5) (Fig. 1).
The evolution of string states are calculated in the path integral formulation by summing up all string configurations connecting the initial to the final string state. The action is proportional to the area of the worldsheet and the proportionality constant, g, is a # Ph.D. student 34 combination of the string tension and the AdS radius. It plays the role of the inverse of the Planck constant as quantum corrections go with inverse powers of g.
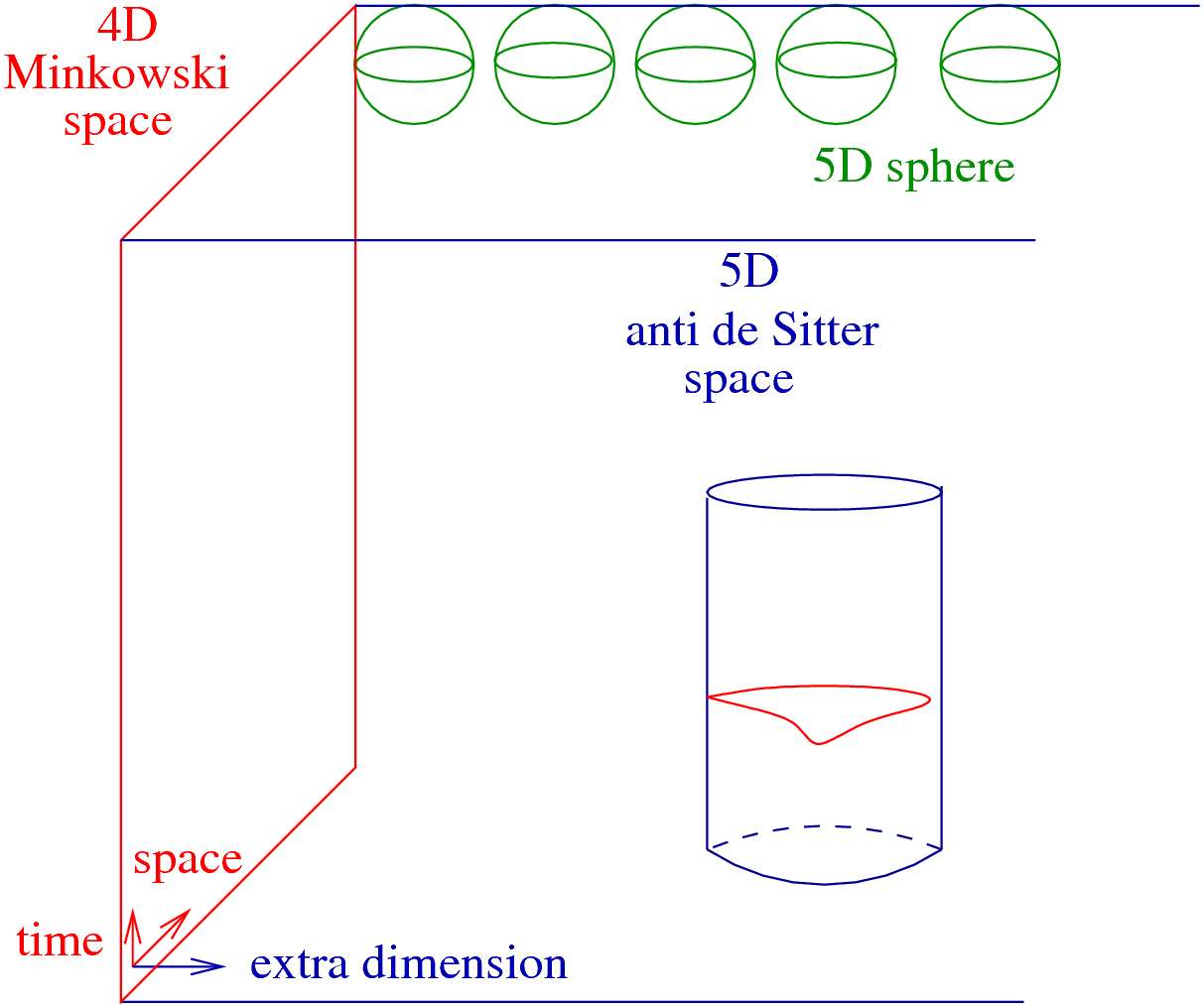
Figure 1. In the holographic description our 4D Minkowski space, indicated by red on the figure, is the holographic boundary of the 5D anti de Sitter space (blue): AdS5. Above each point a 5D sphere is added (green): S5. The evolution of a closed string state is shown. The 2D surface swept by the moving strings is called the worldsheet. The dynamics tries to minimize the area of this worldsheet.
On the other side of the duality we have the simplest interacting 4D SU(N) gauge theory, where N denotes the number of colors (3 for QCD). It has the maximal amount of (super) symmetry and considered to be the hydrogen atom of all gauge theories. Due to the large amount of symmetry all fields are N by N traceless matrices, which create massless particles, whose couplings are completely fixed up to an overall coupling constant gYM. The theory is invariant not only under scale transformations but also under conformal transformations, i.e. coordinate transformations that preserve angles. In conformal invariant theories the small volume, ultraviolet, and the large volume, infrared scales can be mapped to each other thus they manifest the same physical phenomena. In particular, the scattering matrices of the massless particles can be mapped to the vacuum expectation values of lightlike Wilson loops. These Wilson loops can be obtained by drawing consecutively the particles’ momenta and momentum conservation guaranties, that the lines close forming a light-like polygon.
In perturbation theory the ‘t Hooft coupling, λ=N(gYM)2 measures the number of loops, while 1/N the genus, that is adding one more handle on the surface introduces a factor 1/N. Forweak couplings it is enough to sum a few diagrams with a few vertex, however at strong couplings dense surfaces of Feynman graphs contribute dominantly. The intuitive understanding of the duality is that the gauge theory dynamics tries to minimize the surface of dense Feynmann graphs like if it were a string worldsheet in the AdS5xS5 background. It is conjectured that the 't Hooft coupling is related to the string tension as g= λ/(2π). This actually shows why the duality is a conjecture, since perturbative gauge theory provides an expansion for small g, while the quantization of classical strings is an expansion in 1/g.
In the case of gluon scattering amplitudes perturbative calculations are reliable at small couplings. At strong couplings, however, we can use the dual picture and calculate the vacuum expectation value of the light-like polygonal Wilson loop. This is equivalent to the determination of the minimal surface, which can be spanned over the polygon, similarly how, the soup film stretches over the frame (Fig.2).
The shape of the two dimensional surface is dictated by the dynamics of strings. As string theory on the AdS background is integrable, the determination of the minimal surface can be obtained by solving the thermodynamic Bethe ansatz equations of the string sigma model. The analytic expansion of these equations requires the calculation of the masscoupling relation in a multi-scale model.
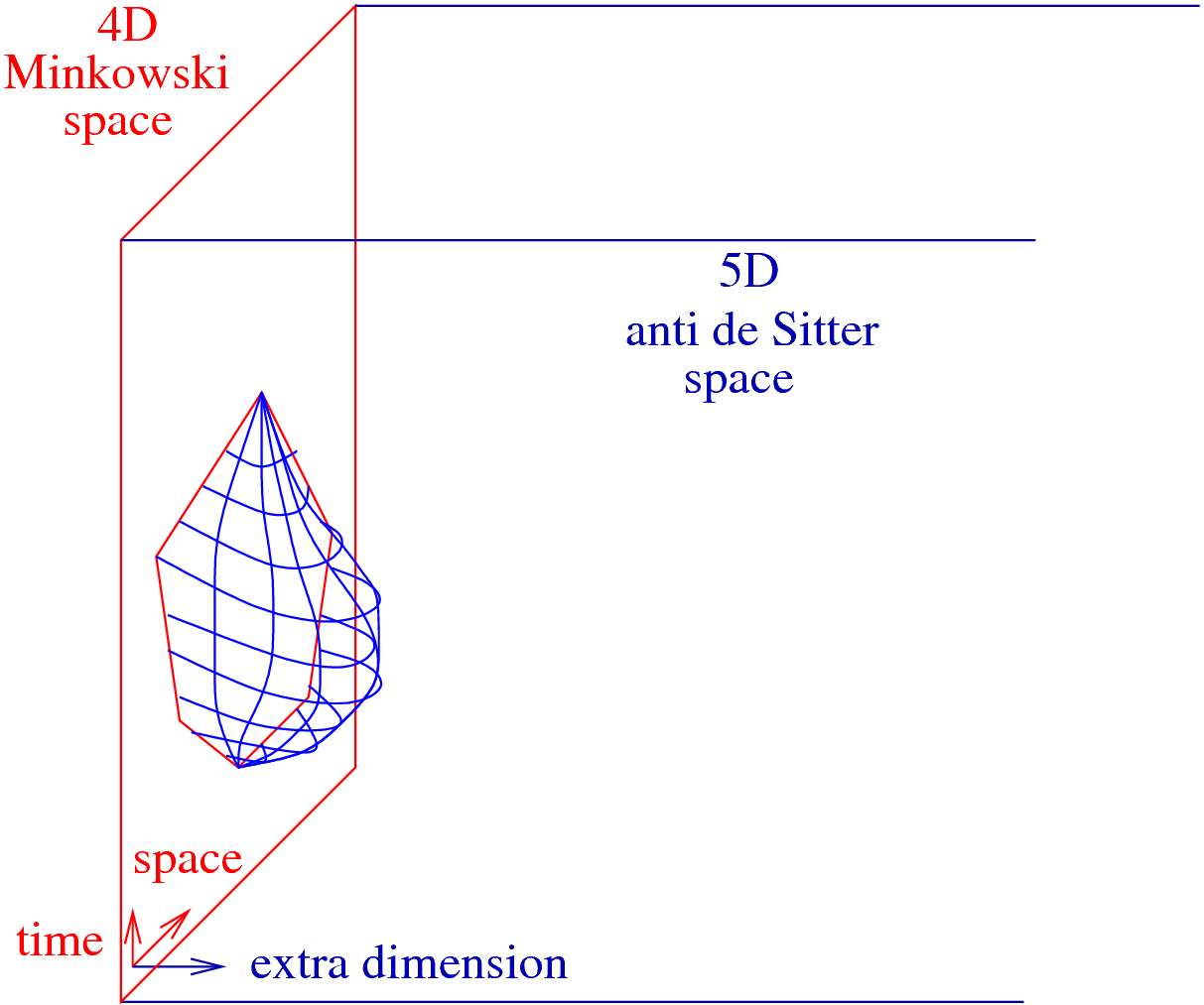
Figure 2. Gluon scattering amplitudes are equivalent to the vacuum expectation values of light-like polygonal Wilson loops, indicated by a red polygon at the Minkowski boundary of AdS space. At strong coupling the amplitude can be calculated by evaluating the area of the minimal surface in AdS space with the boundary polygon, drawn by the blue net.
One of the most difficult problems in a quantum field theory is to determine the masscoupling relation i.e. the relation between the renormalized couplings related to the Lagrangian definition of the theory and the physical masses. Such an exact relation would express for example the dynamically generated nucleon mass in the chiral limit of quantum chromodynamics in units of the perturbative Lambda-parameter Λ. The difficulty lies in the fact that the Lagrangian is defined at short distances (or –UV– scale), while the masses are the parameters at large distances (or –IR– scale).
There is one family of models where such a relation can be found exactly, namely, two dimensional integrable models. The mass/Λ ratio was indeed exactly determined in the nonlinear sigma (NLS) model. To this end, one adds an external field coupled to one of the conserved charges, calculates the free energy perturbatively on the UV side, and compares it to the large field expansion from the Bethe Ansatz integral equation/the thermodynamic Bethe Ansatz (TBA) equation on the IR side.
In contrast to the NLS model with marginally relevant perturbations, there is also a large class of integrable models which can be defined as perturbations of their UV-limiting conformal field theories (CFTs) by strictly relevant scaling operators. In this case, coupling constants are dimensional, and one can show that they are not renormalized in the perturbative CFT scheme and hence are physical themselves. When a model in this class has only one perturbing operator, the relation between the coupling constant and the (lowest) physical mass boils down to a single proportionality constant. This non-trivial constant was determined as well by the method described above for the sine-Gordon and affine-Toda field theories and their reductions.
A common feature of all these models is that they have only one mass scale. In some of these models the particles have a non-trivial spectrum but all mass ratios are encoded in the scattering (S) matrix: the UV/IR relation is complete once the lowest mass is expressed by Λ, the coupling, or some other physical dimensionful parameter related to the Lagrangian. However, when the models have several independent perturbing operators, the particle
spectrum continuously depends on the couplings and not fixed by the S-matrix. In this sense, such models can be called multi-scale, to which the method in the single-scale case is not applicable, and hence there are no results for multi-scale mass-coupling relations in the literature.
The aim of our work was therefore to provide a novel method which can fill this gap. Though our method is conceptually more general, we focused on a class of multi-scale quantum integrable models with strictly relevant perturbations, i.e., the homogenous sine-Gordon (HSG) model. We presented our ideas in particular for its simplest case with two scales. The mass-coupling relation gives the one-point functions of the perturbing operators, encoding
all the non-perturbative information which is not captured by the CFT perturbation. Via the gauge/string duality, it is applied to the four-dimensional maximally supersymmetric gauge theory at strong coupling, which is one of the recent main subjects in field and string theories: it provides the missing link to derive an analytic expansion of the strong-coupling gluon scattering amplitudes.
Results: 2024, 2017-2023
Grants
OTKA K 109312: Holographic solutions of gauge theories (Á. Hegedűs 2013-2016)
OTKA K 116505: Integrability and the holographic duality (Z. Bajnok 2016-2019)
HoloGrav ESF Network: Holographic methods for strongly coupled systems (Z. Bajnok 2012-2016)
“Momentum” Program of the HAS (Z. Bajnok 2012-2017)
International cooperations
MTA Hungarian-Japanese bilateral: Integrability in gauge gravity duality and strong coupling
dynamics of gauge theory II; Kyoto, Tokyo and Tsukuba (Z. Bajnok, 2015-2017)
MTA Hungarian-Polish bilateral: Gauge string duality and its applications; Krakow (Z. Bajnok
2013-2015)
Long term visitor
Ines Aniceto, Krakow, 2016.11.12-2016.12.10
Publications
Articles
1. Aoki S, Balog J, Onogi T, Weisz P: Flow equation for the large N scalar model and
induced geometries. PROG THEOR EXP PHYS 2016:(8) 083B04/1-18 (2016)
2. Bajnok Z, Balog J, Ito K, Satoh Y, Tóth GZ: Exact mass-coupling relation for the
homogeneous Sine-Gordon model. PHYS REV LETT 116:(18) 181601/1-5 (2016)
3. Bajnok Z: How integrability works (for AdS/CFT. ACTA PHYS POL B 47:(12) 2451-2477 (2016)
4. Bajnok Z, Holló L: On form factors of boundary changing operators. NUCL PHYS B 905 96-131 (2016)
5. Bajnok Z, Balog J, Ito K, Satoh Y, Tóth GZ: On the mass-coupling relation of multi-scale
quantum integrable models. J HIGH ENERGY PHYS 2016:(6) 71/1-54 (2016)
6. Bajnok Z, Janik RA: The kinematical AdS(5) x S-5 Neumann coefficient. J HIGH ENERGY
PHYS 2016:(2) 138/1-25 (2016) 37
7. Bajnok Z, Lajer M: Truncated Hilbert space approach to the 2d ϕ 4 theory. J HIGH
ENERGY PHYS 2016:(10) 050/1-41 (2016)
8. Bajnok Z, Nepomechie RI: Wrapping corrections for non-diagonal boundaries in
AdS/CFT. J HIGH ENERGY PHYS 2016:(2) 024/1-23 (2016)
9. Balog J, Zhang P: Effective potential from zero-momentum potential. PROGR THEOR
EXP PHYS 2016:(10) 103B02/1-21 (2016)
10. Gombor T, Palla L: Algebraic Bethe Ansatz for O(2N) sigma models with integrable
diagonal boundaries. J HIGH ENERGY PHYS 2016:(2) 158/1-33 (2016)
11. Hegedűs Á, Konczer J: Strong coupling results in the AdS 5 /CF T 4 correspondence
from the numerical solution of the quantum spectral curve. J HIGH ENERGY PHYS
2016:(8) 061/1-56 (2016)
12. Tóth GZ: Weak cosmic censorship, dyonic Kerr-Newman black holes and Dirac fields.
CLASSICAL QUANT GRAV 33:(11) 115012/1-23 (2016)
Other
13. Pusztai BG, Gorbe TF: Lax representation of the hyperbolic van Diejen dynamics with
two coupling parameters. arXiv:1603.06710v1/1-38 (2016)



