2019
The research team is active in three main different fields: developing new type of i) biomarkers, ii) quantum bits for quantum information processing, and iii) 3rd generation solar cells. István Balogh, Balázs Juhász, Péter Rózsa, János Tamási, Dávid Veres, Ádám Viszoki, Dóra Zalka and Szabolcs Czene mediate the experiments as laboratory assistants. Hanen Hamdi, Vladimir Verkhovlyuk, Philipp Auburger, Anton Pershin and Szabolcs Czene has joined the group in 2019.
Next, we give some highlights of our achievements last year.
Qubits are two-state quantum systems with a low level of interaction with their environments, but still with the ability of being controlled. Paramagnetic point defects in semiconductors are an example, and moreover, if they are also fluorescent as well as their fluorescence intensity depends on the spin state (optically detected magnetic resonance, ODMR), they become spin-optical interfaces, i.e. their spin state can be modified and tested with optical methods. The most interesting such systems are embedded in host materials which have widespread use in semiconductor industry.
Ádám Gali has published back in 2009 his theoretical result that silicon carbide (SiC), a wide-gap semiconductor used in power electronics may contain a point defect of the above type. This point defect is the divacancy defect, an S = 1 paramagnetic qubit with luminescence in the 1100–1300 nanometer infrared range, which is formed when a carbon atom and an adjacent silicon atom are missing from the host lattice. In a tight cooperation with the group of David D. Awschalom (The University of Chicago), our group has considerably contributed to understanding the physics of the divacancy point defect in silicon carbide last year. In these investigations, the host material is 4H-SiC, which is the industrially most-used SiC polytype.
The divacancy point defect can be aligned in four non-equivalent ways in the perfect 4H-SiC layer structure (see fig. 1). Two (PL1, PL2) are high-symmetry (showing threefold rotational symmetry just like in a diamond lattice), and two (PL3, PL4) are low-symmetry (showing only one mirroring symmetry). In an earlier publication of the Awschalom group, experimental results showed two further types (PL5 and PL6 centres with divacancy-like signals).
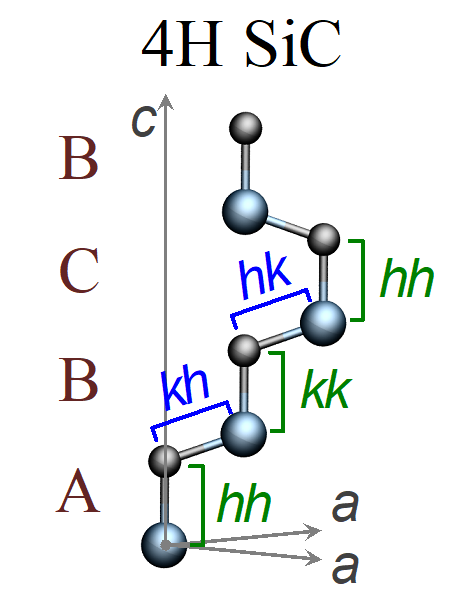
Figure 1. The stacking sequence of 4H-SiC. Every layer is classified as h (hexagonal) or k (cubic) based on its position with respect to the underlying one. The cubic position ensures higher symmetry (locally a diamond-like cubic lattice) at atomic positions. If we eliminate an adjacent pair of a C and a Si atom to generate a divacancy, the adjacent positions in question can be labelled kk, kh, hk, and hh.
Mainly as a work of Viktor Ivády, we have explained PL5 and PL6 with high-precision density-functional-theory calculations . They are divacancy point defects, as previously thought, but embedded in a stacking fault of the 4H-SiC host which is an additional cubic layer instead of a hexagonal one. This stacking fault results in a 0.3 eV deep quantum well in the conduction band, which can trap electrons, and largely alter the photostability of the point defect, which will be an extremely important further property of PL5 and PL6.
This is because divacancy defects in SiC can be ionized by sequential absorption of two photons, via the excited state we also use in their ODMR manipulation. This renders them useless as qubits, and a complicated extra machinery (including a shorter-wavelength laser) is needed to maintain their availability. As it is illustrated in Fig. 2, the PL5 and PL6 defects, however, can be de-ionized with the same wavelength we use for ODMR, and this makes them available for qubit operations almost full-time.
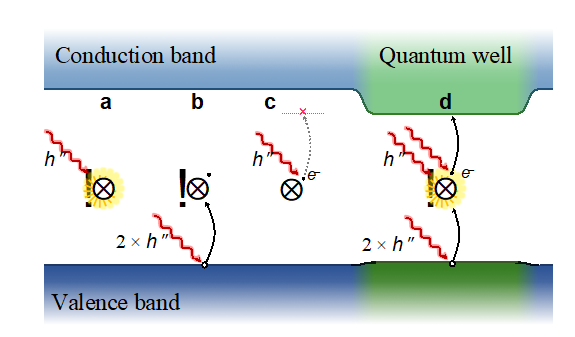
Figure 2. Photoexcitation processes in the PLi centres. a. These divacancy complexes show photoluminescence. b. By absorbing two photons, the centre is ionized, and ceases being a qubit. c. Absobing an additional photon in the ionized state is not enough to get rid of the additional electron in PL1–4 centres. d. Due to the lower CBM edge, an additional photon is enough for de-ionization.
Our cooperation partners at the Linköping University of Sweden have managed to create good samples with PL5 and PL6 defects, and the Chicago University partners at the Argonne National Laboratory examined these samples with their high-resolution X-ray diffraction facility. Their results confirm that PL5 and PL6 defects are associated with cubic stacking faults in 4H-SiC.
PL3 and PL4 defects have been further investigated by the Awschalom group, and they have been shown to exhibit the so-called Landau–Zener–Stückelberg (LZS) interference in the presence of alternating electric field (microwave range), at low temperature, using resonant optical excitation. This is a coherent coupling of the electron spin to the microwave field. The phenomenon has been theoretically explained by calculating the detailed electronic structure of the defect by our research group .
An interesting feature in this process is that the quantization axis of the electron spin is aligned at 70.5 degrees from the hexagonal crystal axis, and the degenerated states are split by the crystal field, which dominates spin-orbit interaction in this case. As a result, the effective model spin Hamiltonian behaves as if the spin quantization axis were a virtual rotational symmetry axis. Using this, the measured LZS interference diagram could be well explained (Fig. 3), and this gives a general strategy to investigate any low-symmetry point-defect qubit.
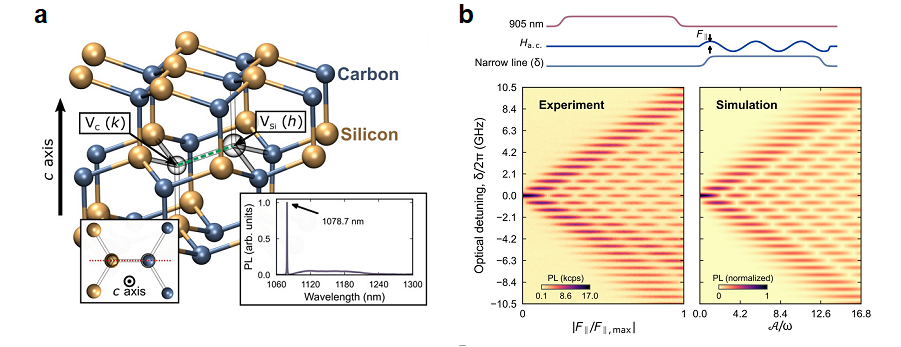
Figure 3. a. PL4 defect configuration in the SiC lattice. The lower right inset shows its photoluminescence spectrum with the ZPL pointed at by the arrow. b. The LZS interference pattern.
In another chief field of our activities, we use density-functional theory calculations to see if other group-IV elements (namely germanium, tin, and lead) paired with a vacancy in a colour centre exhibit similar optical properties to the silicon-vacancy centre in diamond, but with improved spin properties, that permit an economical cooling system. We have developed a new theory for understanding the interaction of light and magnetic fields with these colour centres, and we explore how the dynamical motion of the atoms strongly affects the magneto-optical properties of the defect.
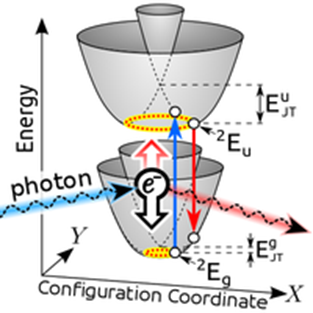
Figure 4. Potential energy surfaces of a vacancy-related dimer complex in diamond. The ellipsoidal minima illustrate the dynamical Jahn-Teller orbits of atoms. Note how the potential energy map changes when the complex gets excited by a photon (or in inverse, when it goes off by emitting another during photoluminescence).
By combining our theory with density-functional theory calculations, we find that lead-vacancy colour centres should have favourable optical and spin properties for operating at room temperature. Mainly as the work of Gergő Thiering, we have developed the model of the so-called dynamical Jahn-Teller effect in these point defects, which gives strong electron-phonon coupling via the dynamic motion of atoms in these systems, (see fig. 4).
In parallel to the theoretical efforts, our experimental group in the Wigner ADMIL laboratory has managed to fabricate and test divacancy centres in tiny SiC nanoparticles. This result can be the basis for future medical applications, for example. Our researchers have filed for a patent on this model technology.



