2017
Superconductivity in layered heterostructures. — During the previous years, a novel and unique computer code was developed which allows us to study the nature of the Andreev bound states related to the proximity effect in normal metal–superconductor heterostructures based on the first-principles Bogoliubov–deGennes (BdG) equations. For the first time, we succeeded in applying the SKKR method for solving the Kohn–Sham–Bogoliubov–deGennes (KSBdG) equation which allowed us to investigate the quasiparticle spectrum of superconducting heterostructures. This year, a fully relativistic generalization of the BdG equations within Multiple Scattering Theory has been derived. The method allows the solution of the first-principles Dirac–Bogoliubov–de Gennes equations combined with a semi-phenomenological parametrization of the exchange-correlation functional. The major difficulty during the development was to derive simple conditions for the case when the right-hand-side and left-hand-side solutions must be treated separately while setting up the corresponding Green function. As an application of the theory, we calculated the superconducting order parameter in Nb/Fe and Nb/Au/Fe systems. We found Fulde–Ferrell–Larkin–Ovchinnikov like oscillations in the iron layers, but more interestingly an oscillatory behaviour is observed in the gold layers as well.
Thin Film Magnetism. — Non-collinear magnetic structures have been investigated in ultrathin films by combining ab initio electronic structure calculations with numerical spin model simulations. The experimentally observed significant increase in the spin spiral period as a function of temperature of three-atomic-layer thick Fe films on Ir(111) has been explained. Ab initio calculations revealed how the addition of hydrogen to a two-atomic-layer thick Fe film on Ir(111) leads to the formation of magnetic skyrmions in place of the spin spiral ground state of the pristine system, in agreement with scanning tunneling microscopy measurements. Theoretical predictions have been made on the characterization of skyrmionic structures with various topological charges.
High Entropy Alloys. — Looking for high-strength and high-temperature-resistant high-entropy alloys (HEAs) new refractory HEA compositions have been predicted theoretically bycombining a refractory CrMoW alloy with late transition metals (LTM = Ni, Co, Fe, and Mn). Ab initio calculations revealed that the LTM additions increase the ductility, but reduce the strength of these CrMoW based alloys with single-phase BCC structure.
The magnetization components of permeability spectra for annealed nanocrystalline (Finemet) core have been studied and four contributions have been revealed for the first time in the literature: i) eddy current; ii) Debye relaxation of magnetization rotation, iii) Debye relaxation of damped domain wall motion and iv) resonant type DW motion. Although the relative weight of these contributions changes with the frequency and exciting field amplitude, the role of eddy current cannot be neglected even for the smallest applied field. These components can be found in the powder cores of soft magnetic composites as well.
Observation of spin-quadrupolar excitations in Sr2CoGe2O7 by high-field electron spin resonance. — When we think of a spin, usually we imagine an arrow pointing somewhere (representing the expectation values of the components of the spin operator), and with the arrow we associate a magnetic moment. Upon time reversal, the arrow reverses its direction. This is a reasonable picture for the spin 1/2 of the electron, but for larger spins this does not exhaust all the possibilities. For example, the dimension of the Hilbert space is 3 for the spin 1, and we can construct spin states for which the expectation values of all the three spin operators vanish — the state does not point anywhere, it cannot be represented by an arrow. The simplest example is the 0 eigenstate of the S2 operator. In fact, there are three linearly independent such states (the zero eigenstate of the Sx, Sy and Sz operators), spanning the Hilbert space. Though they cannot be represented by an arrow, they still break the rotational symmetry, since quadratic forms of spin operators differentiate among them. Instead of arrows, we can use directors (like in the case of liquid crystals), as the rotation by π around an axis perpendicular to the director returns the same state (up to a phase factor). These states are called spin-quadrupoles. Furthermore, these states do not break the time-reversal symmetry.
Similarly, the long-range-ordered states of interacting spins are usually time-reversal-breaking states, with a configuration of “arrows” that repeats itself on the lattice. However, under favorable conditions, interacting spins can produce ordered states where the order parameter is of spin-quadrupolar character which does not break the time reversal symmetry. Theoretically, such phases have been established in spin-one Heisenberg models extended with higher-order spin interactions. Even more interestingly, time-reversal invariant ordered states can also be realized in spin-1/2 systems, where the quadrupole-like order parameter is distributed between two spins on a bond, leading to a so-called nematic ordering.
These theoretical developments have inspired the quest to nematic and quadrupole phases in real materials. However, when relying on standard experimental methods, such phases usually remain hidden. Most of the experimental probes detect spin-dipolar (ΔS=1) transitions, and they do not interact with the spin-quadrupoles, as their detection requires ΔS=2 transitions.
In a collaboration with experimental researchers from Osaka University, we found an unambiguous experimental observation of spin-quadrupolar excitations in the layered Sr2CoGe2O7 multiferroic compound. In this compound, the Co ions are in the centers of tetrahedra formed by the four surrounding O ions (Fig. 1). Since the inversion symmetry is absent, the relativistic spin-orbit coupling allows the coupling of the electric polarizations to the spin-quadrupolar operators. Due to this magnetoelectric coupling present in the Sr2CoGe2O7, the non-magnetic, purely spin-quadrupolar excitation becomes electrically active and detectable by electromagnetic waves, like the electron spin resonance spectroscopy.
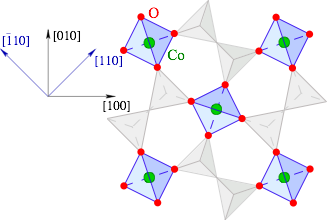
Figure 1. The schematic crystal structure of the Sr2CoGe2O7 multiferroic compound projected onto the ab plane. The green spheres represent the magnetic Co2+ ions with S = 3/2 surrounded by four O2− ions (red) in an alternating tetrahedral environment.
In the electron spin resonance spectra of Sr2CoGe2O7 above the saturation field of 20T, a mode with twice the g-factor of the usual modes is observed (Fig. 2). This indicates the absorption of two magnons, just what is needed for the creation of a quadrupole wave. Indeed, we could explain the features of the experimental spectra taken in different geometries by a simple theoretical model of the spin-quadrupolar wave providing not only a qualitative description, but also a quantitative agreement.
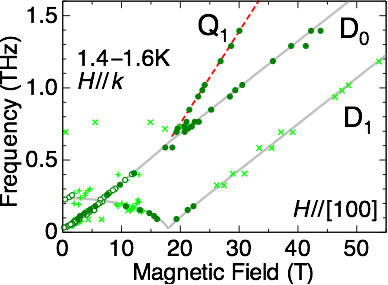
Figure 2. Frequency-field diagrams of the ESR resonance fields of Sr2CoGe2O7 for magnetic fields parallel to the [100] direction of the external magnetic field. The solid lines represent the dipolar resonance modes from the multiboson spin-wave theory. The red dashed line indicates a resonance mode with a slope twice larger than the others, corresponding to a two-magnon excitation — the quadrupolar mode.
The most significant point of our finding is the first observation of non-magnetic spin-quadrupolar excitation in an antiferromagnetic material (Fig. 3). Such quadrupolar degrees of freedom become inherent in systems with larger than S=1/2 magnetic moments, regardless of the presence of magneto-electric coupling. Upon condensing such multipolar excitations, magnetically disordered exotic quantum phases may arise. The experimental identification of quadrupole excitations with vanishing gap gives us a possibility to identify long-sought nematic phases, which stand without any usual magnetic fingerprint and are almost impossible to tell apart from other non-magnetic phases. Furthermore, our work will stimulate the application of the magnetoelectric effect as a spectroscopy tool.
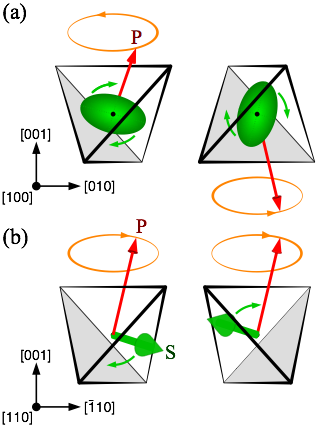
Figure 3. Schematic plot of (a) the Q1 quadrupolar mode for H∥[100] and (b) the dipolar modes for H∥[110], as seen from the direction of the magnetic field. In both cases the oscillating component of the uniform electric polarization P (shown by orange ellipse) is perpendicular to the external magnetic field H, therefore they are active in the Faraday configuration. The green ellipse represents the rotating quadrupolar moments, while the green arrows the precessing dipolar spins on the two sublattices. The red arrows show the electric polarization vectors which are excited by the oscillating electric field.



