2019
Short distance singularity of the nuclear potential. — The characteristic features of the phenomenological nucleon potentials, shown in Fig. 1, are well known. The force at medium to long range is attractive; this feature is due to pion and other heavier meson exchange. The strong repulsive core of the potential at short distances had no satisfactory theoretical explanation until recent advances in lattice QCD simulations made possible to determine the potential in fully dynamical lattice QCD. The results of this first principles calculation resemble the phenomenological potential, including its repulsive core. The short distance behaviour of the potential was subsequently studied also in perturbative QCD. The results of the perturbative calculations [3] show that at extremely short distances the potential behaves as 1/r2 (up to log corrections characteristic to perturbative QCD). Calculations in holographic QCD also give a similar inverse square potential at short distances.
Although the recent theory of low energy nuclear interactions is based on effective chiral field theory (EFT) of mesons and nucleons, the phenomenological potential remains important as a source of intuition and is still often used in the study of multinucleon systems and in the determination of the equation of state for dense nuclear matter as starting point of quantitative work. As can be seen in Fig. 1, the phenomenological potential is not uniquely determined. Nevertheless, known versions more or less agree on its main qualitative features.
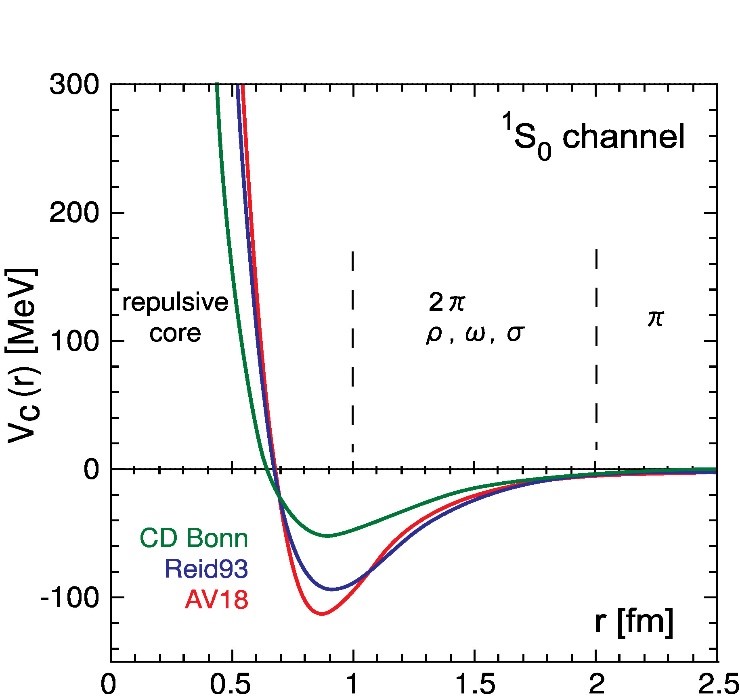
Figure 1. The three most popular phenomenological nucleon potentials.
From a purist viewpoint the notion of nuclear potential does not make much sense below 0.5 fermi for various reasons: the nonrelativistic quantum-mechanical description based on the Schrödinger equation cannot work beyond about 350 MeV laboratory energy because it cannot incorporate particle production; relativistic effects become important at the corresponding energy range; finally the composite nature of nucleons becomes relevant at distances comparable to their size. Therefore, a meaningful reconstruction of an effective nuclear potential must be based on experimental data in the 0 < ELAB < 350 MeV energy range. This leads to the problem of quantum inverse scattering with incomplete data.
Inverse scattering with incomplete data [1]. — In the theory of inverse scattering with incomplete data the lack of full information on the scattering phase shifts is (partially) compensated by other, additional pieces of information. In this paper we concentrate on the singular core of the potential and assume it behaves for small r as U(r) =n(n+1)/r2, where the parameter n is non-negative (repulsive core). In a recent paper [2] we studied the singular behaviour of the nucleon potential in the 1S0 channel and in the 3S1-3D1 coupled channels. Assuming a rational, Bargmann type S-matrix, a 1/r2 asymptotic behaviour naturally emerges. In this method the incompleteness of the scattering data is compensated by the assumption on the rational form of the S-matrix. For Bargmann-type S-matrices the strength parameter n can only take integer values.
However, on physical grounds, there is no reason why the effective strength parameter n should be integer. In the paper [1] we undertook a systematic study of the strength parameter n in various np scattering channels assuming the n(n+1)/r2 form but not requiring n integer. We use the Marchenko method of quantum inverse scattering because this efficient method is applicable to all type of potentials (not necessarily of Bargmann-type). In case of Bargmann potentials the Marchenko method has the extra advantage that the results can be obtained purely algebraically [2]; in other cases it requires the solution of a linear integral equation. Quantum inverse scattering, the problem of finding the potential from scattering data, is completely solved in a mathematically precise way. The potential can be uniquely reconstructed, if full information on scattering at all energies and some additional data related to bound states (binding energies and asymptotic decay constants) are all available. Since this is rarely the case, we worked out a method to extrapolate limited range data.This is possible because the asymptotic large energy behaviour is intimately related to the singularity strength via the generalized Levinson's theorem.
We undertook a systematic study of the n parameter for various low angular momentum partial waves of np scattering: in the 1S0, 3P1, 3P0 and 3D2 channels. We constructed the potential in each channel with a 1/r2 type singular behaviour based on experimental data below 350 MeV LAB energy and extrapolated with some n. We determined the best choice for n. We found that the singularity of the central potential in the 1S0 channel (see Fig. 2) is best approximated by n= 2:0, an integer. But the best choice for the 3P1, 3P0, 3D2 channels turn out to be n = 2:3, n = 3:2, n= 2:3, respectively.
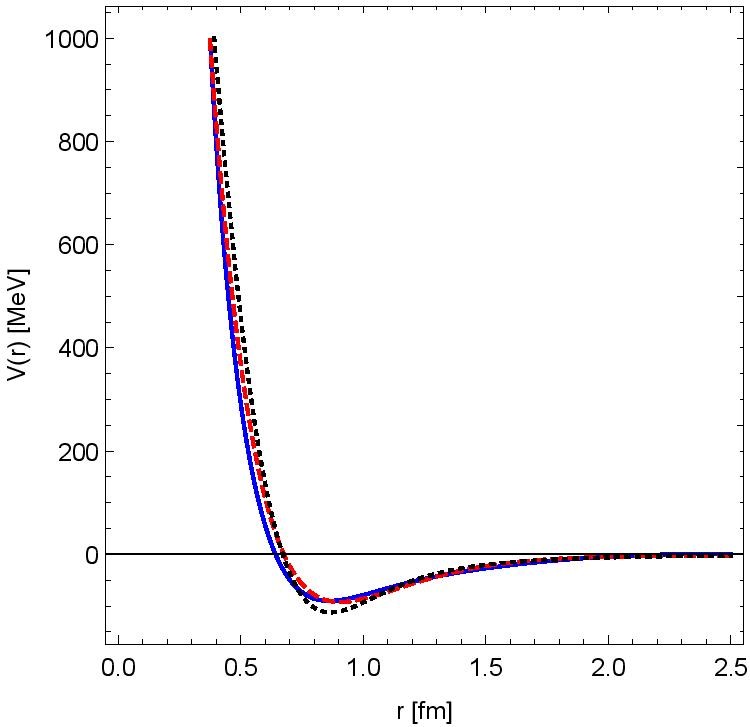
Figure 2. Reconstruction of the 1S0 channel central potential. The solid (blue) line is the potential obtained with our extrapolation method, the dashed (red) line is the Reid93 potential, and the AV18 potential is dotted (black).



