Egykristályok röntgen szabadelektron lézer keltette Kossel-vonal mintázatának pillanatszerű, párhuzamos mérése teszi lehetővé a 3 dimenziós atomszerkezet femtoszekundumok alatt történő meghatározását.
Az atomok elrendeződése egy szilárd anyagban döntő fontosságú az anyag tulajdonságainak megértéséhez. Kristályok atomi szerkezetének első, és ma is széles körben használt kísérleti módszere a röntgendiffrakció. Egy diffrakciós méréshez szükséges időt a meghatározandó szerkezet bonyolultsága, a kristály mérete, a kísérleti technika és a röntgennyaláb tulajdonságai együtt határozzák meg. A 4. generációs röntgenforrások, a röntgen szabadelektron lézerek (XFEL) egyetlen, néhány fs (10-15s) időtartamú impulzusban, nagyságrendileg ugyanannyi felhasználható röntgen fotont biztosítanak, mint egy több órán át folyamatosan üzemelő laboratóriumi röntgenforrás. Ennek tükrében azt gondolhatnánk, hogy a diffrakciós mérés elvégzésének időtartama ennek megfelelően lecsökkenthető. De ez nem így van. Egy hagyományos egykristálydiffrakciós mérést nem lehet tetszőlegesen lerövidíteni és egyetlen XFEL-impulzus segítségével elvégezni. Ennek oka, hogy a Bragg-reflexiókat általában sorban rögzítik, miközben a kristályt forgatják a beeső nyalábban. Azonban a kristály orientációjának megváltoztatására – különösen kontrollált módon – femtoszekundumok alatt nincs lehetőség.
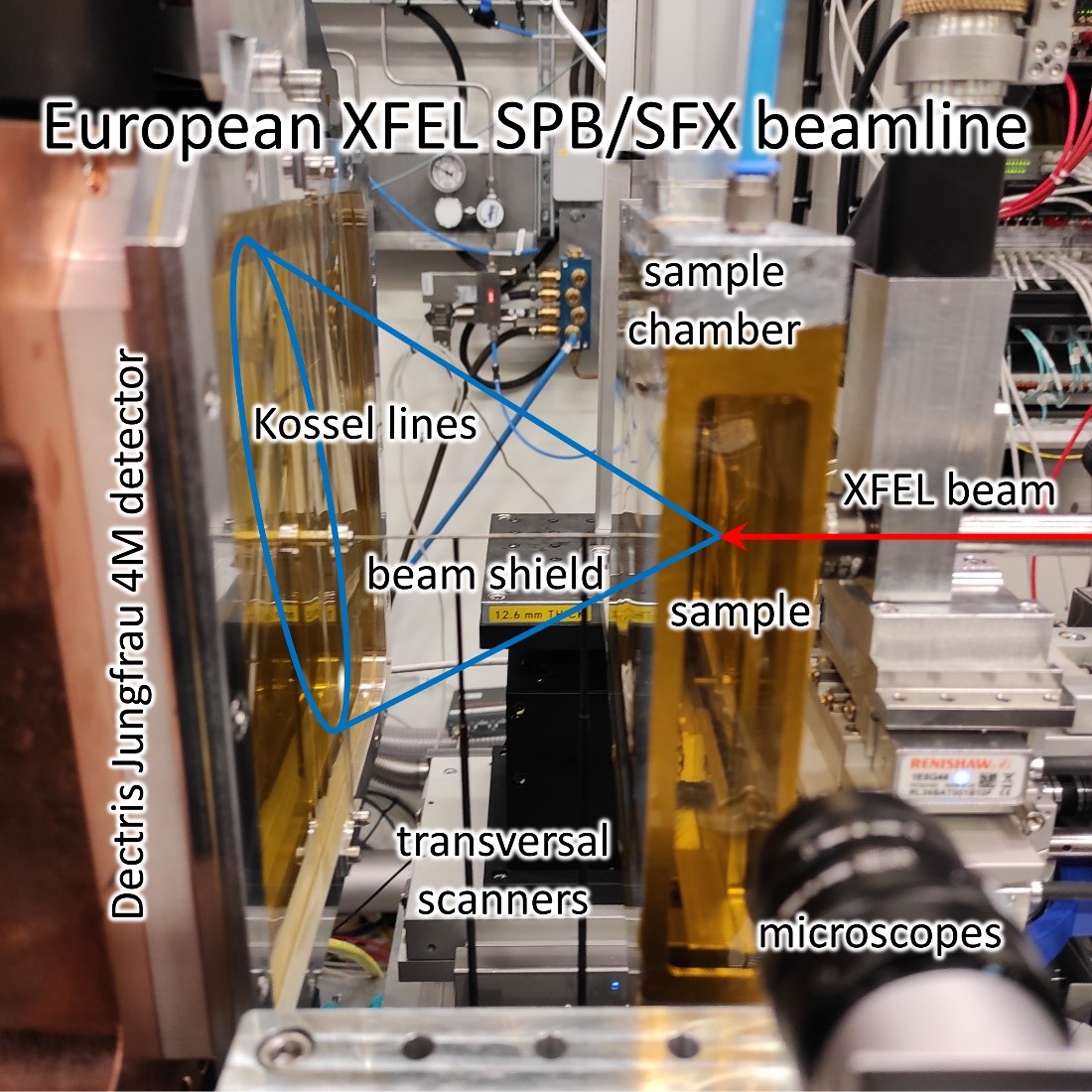
A Nature Communications folyóiratban megjelent publikációban Bortel Gábor, Tegze Miklós és Faigel Gyula bemutatott és demonstrált egy olyan kísérleti technikát, amely egy egykristály nagyszámú Bragg-reflexióját méri párhuzamosan, a minta forgatása nélkül. Így egyetlen XFEL-impulzus segítségével is lehetséges meghatározni a kristály teljes 3 dimenziós szerkezetét. Ez a módszer a röntgenkutatás hajnalán már megfigyelt és megmagyarázott Kossel-vonalakra támaszkodik: Az eljárás során egy másodlagos röntgenforrás gömbhullám sugárzási tere "minden irányból" éri a kristály síkjait, – ezzel kiküszöbölve a kristály forgatásának igényét – de csak a Bragg-feltételt kielégítő komponensek reflektálódnak, és alkotnak egy kúp alakú sugárzási teret, amely elhagyja a mintát. A másodlagos forrás maga a kristály néhány atomja, amelyeket az XFEL-impulzus gerjeszt, és azok valamivel alacsonyabb röntgen-energián fluoreszcens sugárzást bocsátanak ki. Mivel ezek a belső forrásatomok a kristályszerkezet részét képezik, elhelyezkedésük azonos az összes elemi cellában, ami a Kossel-vonalak intenzitásprofiljában egy interferencia jelet is eredményez, amely az adott reflexió szerkezeti tényezőjének fázisát is kódolja.
Az európai XFEL létesítményben végzett demonstrációs kísérletben egyetlen ~25 fs hosszú, ~1 mJ energiájú XFEL-impulzus gerjesztette GaAs és GaP egykristály minták Ga atomjait, és a Kossel-vonalak kúpszeletek formájában jelentek meg egy sík detektor felületén. A minták félvezető minőségű egykristályok vékonyított szeletei voltak a nagy kontrasztú, jó minőségű Kossel-vonalakat mérése érdekében. A minta másodlagos forrásatomjainak fluoreszcens sugárzása által kialakított Kossel-vonal mintázatot egy az impulzus idejére integráló 4 MPixeles detektor rögzítette.

A Kossel-vonal mintázat mindenekelőtt geometriai információt tartalmaz. A kúp tengelye és nyílásszöge minden egyes Kossel-vonal esetében egy reciprok rácsvektort definiál, és végső soron meghatározza a kristályrácsot. A felvett mintázat megfelelően nagy szögfelbontásának köszönhetően a finom interferenciajel lehetővé teszi a szerkezeti tényezők amplitúdójának és fázisának meghatározását is. Ez az információ a fázisprobléma elegáns megoldásához vezet, mivel az elemi cellán belüli elektronsűrűség Fourier-szintézissel meghatározható.
Az új mérési elv kigondolása és gyakorlati megvalósítása új lehetőségeket jelent az extrém körülmények hatására rövid ideig létrehozható szerkezeti átalakulások vizsgálatában, vagy lehetővé teszi a pumpa-próba mérések során a teljes szerkezetmeghatározást minden egyes próbaimpulzus esetében. Ezeken túl az eredmények jelentősége abban rejlik, hogy az új mérési elv következtében egy teljes mérés pillanatszerűen elvégezhető, és a módszer a fázisprobléma megoldására is lényegesen új, kísérleti információn alapuló megoldást kínál.



