A Wigner Kollokvium következő előadója Miroslav Grmela kanadai elméleti fizikus. Előadására október 1-én kedden 14 órakor kerül sor az 1-es épület Tanácstermében. Előadásának címe: A termodinamika összeköti a modellezés szintjeit (Thermodynamics Relates Levels of Description)
Az előadás összefoglalója:
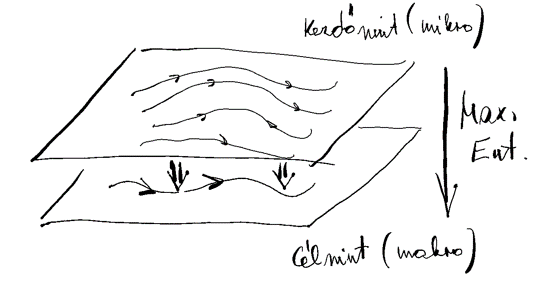
Hilbert 6. problémája, a fizika axiomatizálása, egyike azoknak, amelyet ma is megoldatlannak tartunk. Ennek egy szűkített változata a kinetikus gázelmélet és a kontinuumelmélet, azaz a mikroszkopikus és makroszkopikus elméletek viszonyának matematikailag szigorú tárgyalása. Az előadás bemutatja, hogy termodinamikai-geometriai struktúrák milyen szerepet játszanak a különböző szintű fizikai modelljeinek szisztematikus összekapcsolásában. Végül megemlítjük a termodinamika lehetséges szerepét a mesterséges intelligenciával kapcsolatban. (szöveg és ábra Ván Péter)
Az előadás összefoglalója:(angolul)
The starting level (SL) and the target level (TL) are two levels of description of macroscopic systems. If both levels are autonomous and (SL) takes into account more details than (TL) then there exists a way to prepare the macroscopic systems for the (TL) level and the preparation process is seen in the time evolution that takes place in (SL). For example, if (TL) is the level of the classical equilibrium thermodynamics then the existence of the preparation process is called a zero law of thermodynamics. If (SL) is, for example, the level of kinetic theory and the macroscopic system under investigation is an externally unforced ideal gas then the time evolution describing the preparation process is governed by the Boltzmann kinetic equation. If (TL) remains to be the level of the classical equilibrium thermodynamics but (SL) is a general autonomous level and the macroscopic system is a general externally unforced macroscopic system then the time evolution describing the passage (SL) → (TL) is governed by an abstract Boltzmann equation (called also GENERIC). The time evolution generated by the abstract Boltzmann equation is shown to be a sequence of infinitesimal Legendre transformations. The level (TL) emerges as a pattern in the collection of all trajectories generated by the abstract Boltzmann equation (as a pattern in the (SL)-phase portrait). The level (TL) emerges completely when a potential (called an entropy), that increases during the time evolution, reaches its maximum. The geometry of the manifold ((TL)-manifold) composed of the states in the (SL) state space that are reached as t → ∞ represents the (TL)- fundamental thermodynamic relation implied by the passage (SL) → (TL). The vector field attached to the (TL)-manifold represents the (TL)-vector field that is reduced from the (SL)-vector field. If the level (TL) is the level of equilibrium thermodynamics then the (TL)-vector field is a zero vector field. In the case when the macroscopic systems are externally forced then the level of equilibrium thermodynamics is inaccessible and (TL) is a mesoscopic level on which the time evolution generated by the (TL)-vector field takes place. The potential driving the passage (SL) → (TL) in the space of (SL)-vector fields is not entropy but a dissipation potential that is closely related to the entropy production. A possible role that thermodynamics can play in AI is also discussed.
Az előadás Zoomon is követhető:
https://wigner-hu.zoom.us/j/86872318081?pwd=xzYwgIyL5Sm0b2bnDucOdywMqvP…
Meeting ID: 868 7231 8081
Passcode: 784748
Röviden az előadóról:
Miroslav Grmela elméleti fizikából szerzett diplomát a Prágai Műszaki Egyetemen, majd PhD fokozatot a Csehszlovák Tudományos Akadémián, ahol a neutron transzport elméletét tanulmányozta. Jelenleg a Cseh Tudományos Akadémia Nukleáris Kutatóintézetének, a vancouveri Brit Columbia Egyetemnek és a Polytechnique Montréal kutatója. Kutatási területe a kinetikus elmélet, a komplex folyadékok mechanikája, a többskálájú dinamika, és a legfőképpen a nemegyensúlyi termodinamika. Az ő nevéhez fűződik a nemegyensúlyi termodinamika GENERIC (General Equation for Non-Equilibrium Reversible-Irreversible Coupling) elméletének a kidolgozása.



